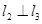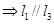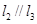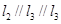题目内容
.正方体ABCD-A1B1C1D1中,E、F分别AB、C1D1的中点,则A1B1与平面A1EF所成角的正切值为
A.2 B.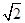 C.1 D.
C.1 D.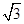
A.2 B.
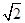 C.1 D.
C.1 D.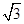
B
解:由题可知,EF⊥平面A1B1C,又EF?平面A1EF,
∴平面A1B1C⊥平面A1ECF.∴B1在平面A1ECF上的射影在线段A1C上.
∴∠B1A1C就是A1B1与平面A1EF所成的角.
∵A1B1⊥B1C,在Rt△A1B1C中,tan∠B1A1C=B1C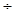 A1B1 =
A1B1 =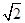 .
.
∴A1B1与平面A1EF所成角的正切值为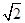 ,选B.
,选B.
∴平面A1B1C⊥平面A1ECF.∴B1在平面A1ECF上的射影在线段A1C上.
∴∠B1A1C就是A1B1与平面A1EF所成的角.
∵A1B1⊥B1C,在Rt△A1B1C中,tan∠B1A1C=B1C
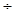 A1B1 =
A1B1 =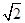 .
.∴A1B1与平面A1EF所成角的正切值为
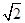 ,选B.
,选B.
练习册系列答案
相关题目
 中,
中,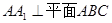 ,
,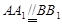 ,
,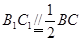 ,
,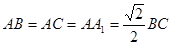 。
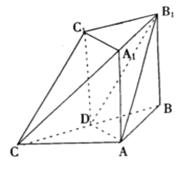
。
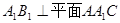 ;
;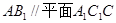 ;
;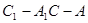 的余弦值。
的余弦值。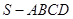 中,
中,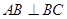 ,
,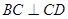 ,侧面
,侧面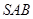 为等边三角形,
为等边三角形,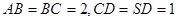 .
.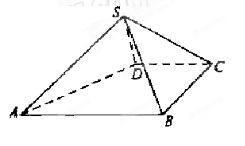
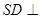 平面
平面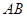 与平面
与平面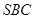 所成角的正弦值.
所成角的正弦值.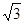 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.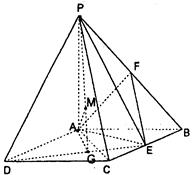
 的底面边长为
的底面边长为 ,
, 为
为 中点.
中点.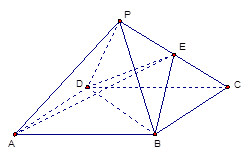
 //平面
//平面 ;
; 是二面角
是二面角 的平面角,求直线
的平面角,求直线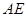 与平面
与平面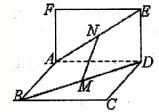
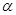 ∥平面
∥平面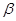 ,
,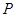 是
是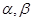 外一点,过点
外一点,过点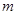 与
与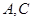 ,过点
,过点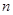 与
与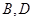 且
且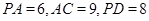 ,则
,则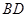 的长为
的长为 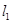 ,
,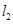 ,
,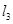 是空间三条不同的直线,则下列命题正确的是( )
是空间三条不同的直线,则下列命题正确的是( )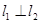 ,
,