题目内容
如图,空间中两个有一条公共边AD的正方形ABCD和ADEF.设M、N分别是BD和AE的中点,那么
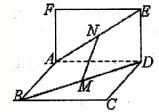
①AD⊥MN;②MN∥平面CDE;③MN∥CE;④MN、CE异面
以上4个命题中正确的是

①AD⊥MN;②MN∥平面CDE;③MN∥CE;④MN、CE异面
以上4个命题中正确的是
1,2,3
:(1)取AD的中点H,连接NH,MH则NH//DE,NH=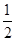 DE,MH//CD, MH=
DE,MH//CD, MH=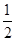 CD
CD
又AD⊥DE,AD⊥CD所以AD⊥NH,AD⊥MH又NH∩MH="H" 所以AD⊥面MHN 所以AD⊥MN 所以(1)正确(2)由(1)知NH//DE,NH=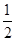 DE,MH//CD, MH=
DE,MH//CD, MH=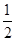 CD则面MHN∥面CDE 又MN?面MHN 所以MN∥平面CDE 所以(2)正确
CD则面MHN∥面CDE 又MN?面MHN 所以MN∥平面CDE 所以(2)正确
(3)连接AC则AC过点M 在三角形ACE中M,N为中点所以MN∥CE 所以(3)正确,(4)错,故答案为:①②③
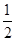 DE,MH//CD, MH=
DE,MH//CD, MH=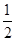 CD
CD又AD⊥DE,AD⊥CD所以AD⊥NH,AD⊥MH又NH∩MH="H" 所以AD⊥面MHN 所以AD⊥MN 所以(1)正确(2)由(1)知NH//DE,NH=
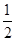 DE,MH//CD, MH=
DE,MH//CD, MH=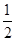 CD则面MHN∥面CDE 又MN?面MHN 所以MN∥平面CDE 所以(2)正确
CD则面MHN∥面CDE 又MN?面MHN 所以MN∥平面CDE 所以(2)正确(3)连接AC则AC过点M 在三角形ACE中M,N为中点所以MN∥CE 所以(3)正确,(4)错,故答案为:①②③

练习册系列答案
相关题目
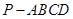 底面是平行四边形,面
底面是平行四边形,面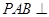 面
面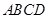 ,
,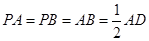 ,
, ,
,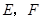 分别为
分别为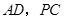 的中点.
的中点.
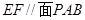 ;
;  的余弦值.
的余弦值.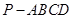 中,底面
中,底面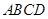 为平行四边形,
为平行四边形,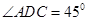 ,
,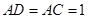 ,
,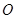 为
为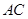 中点,
中点,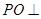 平面
平面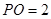 ,
,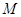 为
为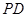 中点.
中点.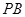 //平面
//平面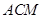 ;
;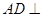 平面
平面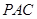 ;
;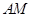 与平面
与平面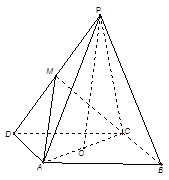
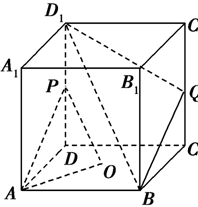
 中,
中, 为底面
为底面 的中心,
的中心,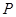 是
是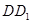 的中点,设
的中点,设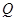 是
是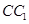 上的中点,求证:(1)
上的中点,求证:(1)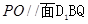 ;
;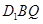 ∥平面
∥平面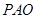 .
.
 中,
中,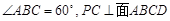 ,
,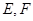 是
是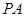 和
和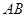 的中点.(Ⅰ)求证:
的中点.(Ⅰ)求证: 平面
平面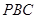 ;
;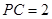 ,求
,求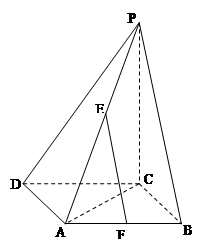
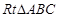 中,
中,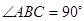 ,
,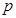 为△ABC所在平面外一点,PA⊥面ABC,则四面体P-ABC中共有直角三角形个数为
为△ABC所在平面外一点,PA⊥面ABC,则四面体P-ABC中共有直角三角形个数为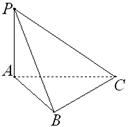
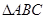 内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:①
内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:①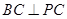 ;②
;②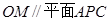 ;③点A到平面PBC距离就是△PAC的PC边上的高.④二面角P-BC-A大小不可能为450,其中真命题的个数为 ( )
;③点A到平面PBC距离就是△PAC的PC边上的高.④二面角P-BC-A大小不可能为450,其中真命题的个数为 ( )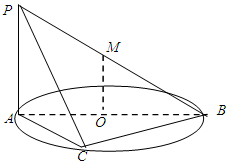
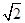 C.1 D.
C.1 D.