题目内容
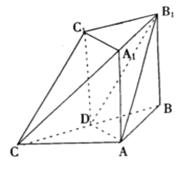
如图:在多面体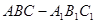 中,
中,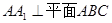 ,
,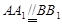 ,
,
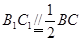 ,
,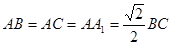 。
。
(1)求证: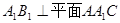 ;
;
(2)求证: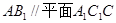 ;
;
(3)求二面角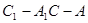 的余弦值。
的余弦值。
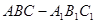 中,
中,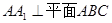 ,
,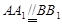 ,
,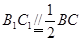 ,
,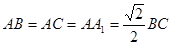 。
。
(1)求证:
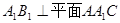 ;
;(2)求证:
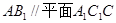 ;
;(3)求二面角
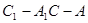 的余弦值。
的余弦值。(1)见解析(2) 见解析(3)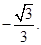
本试题主要是考查了线面垂直和线面平行的判定定理的运用,以及二面角大小的求解的综合运用。
(1)yw由于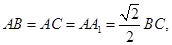 所以
所以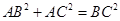 ,
,
则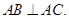 又
又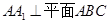 ,则
,则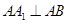 是解题的关键
是解题的关键
(2) 取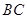 的中点
的中点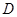 ,连结
,连结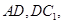
由条件知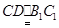 ,
,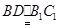 ,
,
∴四边形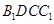 和
和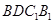 为平行四边形,
为平行四边形,
∴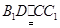 ,
,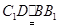 ,∴
,∴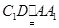 ,
,
∴四边形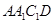 为平行四边形,∴
为平行四边形,∴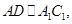
然后得到结论。
(2)建立空间直角坐标系,然求解平面的法向量的坐标,结合向量的数量积的性质得到夹角的值。
证明:(Ⅰ)由于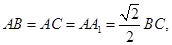 所以
所以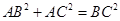 ,
,
则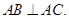 又
又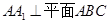 ,则
,则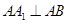 ,
,
所以 又
又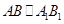 ,则
,则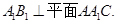
(Ⅱ)取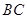 的中点
的中点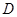 ,连结
,连结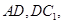
由条件知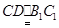 ,
,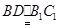 ,
,
∴四边形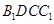 和
和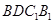 为平行四边形,
为平行四边形,
∴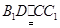 ,
,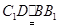 ,∴
,∴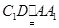 ,
,
∴四边形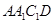 为平行四边形,∴
为平行四边形,∴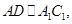
∴平面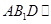 平面
平面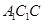 ,则
,则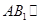 平面
平面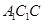 。
。
(Ⅲ)由(Ⅰ)知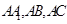 两两垂直,如图建系,
两两垂直,如图建系,

设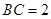 ,则
,则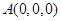 ,
,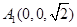 ,
,
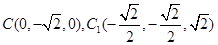 ,
,
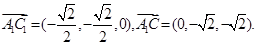
设平面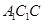 的法向量为
的法向量为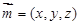 ,则由
,则由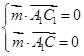 ,得
,得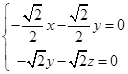 ,取
,取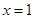 ,则
,则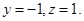 故
故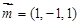 ,
,
而平面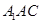 的法向量为
的法向量为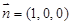 ,则
,则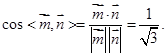
所以二面角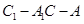 为钝二面角,故二面角
为钝二面角,故二面角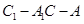 的余弦值为
的余弦值为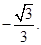
(1)yw由于
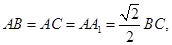 所以
所以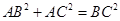 ,
,则
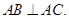 又
又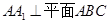 ,则
,则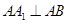 是解题的关键
是解题的关键(2) 取
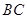 的中点
的中点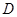 ,连结
,连结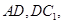
由条件知
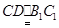 ,
,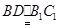 ,
,∴四边形
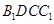 和
和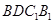 为平行四边形,
为平行四边形,∴
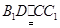 ,
,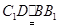 ,∴
,∴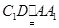 ,
,∴四边形
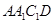 为平行四边形,∴
为平行四边形,∴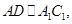
然后得到结论。
(2)建立空间直角坐标系,然求解平面的法向量的坐标,结合向量的数量积的性质得到夹角的值。
证明:(Ⅰ)由于
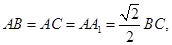 所以
所以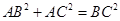 ,
,则
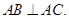 又
又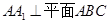 ,则
,则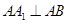 ,
,所以
 又
又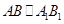 ,则
,则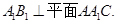
(Ⅱ)取
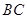 的中点
的中点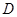 ,连结
,连结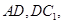
由条件知
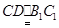 ,
,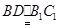 ,
,∴四边形
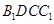 和
和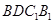 为平行四边形,
为平行四边形,∴
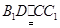 ,
,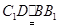 ,∴
,∴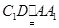 ,
,∴四边形
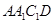 为平行四边形,∴
为平行四边形,∴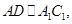
∴平面
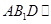 平面
平面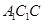 ,则
,则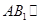 平面
平面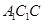 。
。(Ⅲ)由(Ⅰ)知
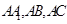 两两垂直,如图建系,
两两垂直,如图建系,
设
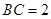 ,则
,则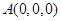 ,
,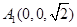 ,
,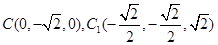 ,
,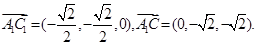
设平面
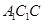 的法向量为
的法向量为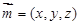 ,则由
,则由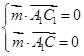 ,得
,得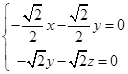 ,取
,取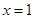 ,则
,则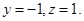 故
故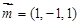 ,
,而平面
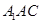 的法向量为
的法向量为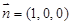 ,则
,则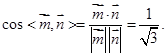
所以二面角
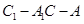 为钝二面角,故二面角
为钝二面角,故二面角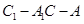 的余弦值为
的余弦值为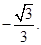

练习册系列答案
相关题目
 中,
中, ,
, 是
是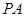 和
和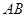 的中点.(Ⅰ)求证:
的中点.(Ⅰ)求证: 平面
平面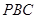 ;
;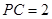 ,求
,求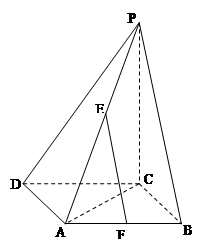
 中,
中,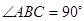 ,
, 为△ABC所在平面外一点,PA⊥面ABC,则四面体P-ABC中共有直角三角形个数为
为△ABC所在平面外一点,PA⊥面ABC,则四面体P-ABC中共有直角三角形个数为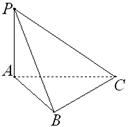
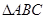 内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:①
内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:①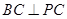 ;②
;②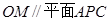 ;③点A到平面PBC距离就是△PAC的PC边上的高.④二面角P-BC-A大小不可能为450,其中真命题的个数为 ( )
;③点A到平面PBC距离就是△PAC的PC边上的高.④二面角P-BC-A大小不可能为450,其中真命题的个数为 ( )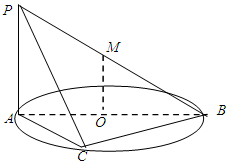
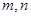 与平面
与平面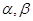 ,有以下四个命题:
,有以下四个命题: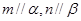 且
且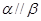 ,则
,则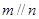 ;
;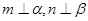 且
且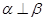 ,则
,则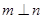 ;
;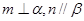 且
且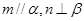 且
且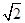 C.1 D.
C.1 D.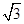
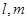 ,平面
,平面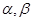 ,且
,且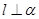 ,
,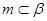 ,给出下列四个命题:
,给出下列四个命题: ∥
∥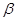 ,则
,则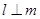 ;②若
;②若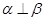 ,则
,则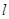 ∥
∥ ;④若
;④若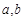 是不同的直线,
是不同的直线,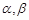 是不同的平面,若①
是不同的平面,若①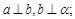 ②
②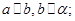 ③
③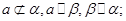 ④
④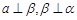 ,则其中能使
,则其中能使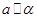 的充分条件的个数为( )
的充分条件的个数为( ) ,
,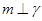 ,那么必有( )
,那么必有( )