题目内容
(本小题8分)已知三棱锥A—BCD及其三视图如图所示.
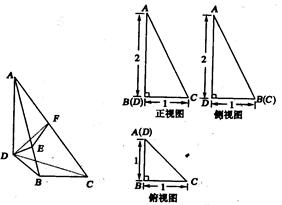
(1)求三棱锥A—BCD的体积与点D到平面ABC的距离;
(2)求二面角 B-AC-D的正弦值.

(1)求三棱锥A—BCD的体积与点D到平面ABC的距离;
(2)求二面角 B-AC-D的正弦值.
(1) 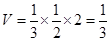 ;(2)二面角 B-AC-D的正弦值是
;(2)二面角 B-AC-D的正弦值是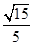 。
。
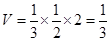 ;(2)二面角 B-AC-D的正弦值是
;(2)二面角 B-AC-D的正弦值是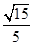 。
。考查线面平行、线线垂直的判定定理以及体积的求解.涉及到的知识点比较多,知识性技巧性都很强,属于中档题
(1)利用三视图可知△ABC为直角三角形,∠DBC为直角,AD⊥面DBC,DB=BC=1,AD=2,则DE的长为点D到面ABC的距离,以及三棱锥的体积可得。
(2)作DF⊥AC于点F,连结EF,
∵DE⊥面ABC ∴DE⊥AC ∴AC⊥面DEF ∴AC⊥EF
∴∠DFE是二面角 B-AC-D的平面角从而解三角形可知。
(1)
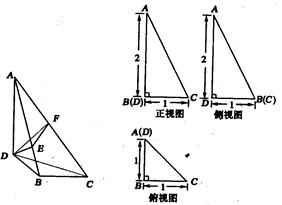
由三视图可得△ABC为直角三角形,∠DBC为直角,AD⊥面DBC,DB=BC=1,AD=2…………….2分
作DE⊥AB于点E
∵AD⊥面DBC,∴AD⊥BC
∵∠DBC为直角 ∴BC⊥面ADB
∴BC⊥DE
∴DE⊥面ABC………3分
∴DE的长为点D到面ABC的距离
∵DB=1,AD=2 ∴DE=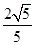 ∴点D到平面ABC的距离为
∴点D到平面ABC的距离为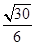 ………4分
………4分
∵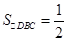 ,∴
,∴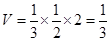 ………5分
………5分
(2) 作DF⊥AC于点F,连结EF,
∵DE⊥面ABC ∴DE⊥AC ∴AC⊥面DEF ∴AC⊥EF
∴∠DFE是二面角 B-AC-D的平面角………7分
∵DB="BC=1" ∴DC=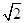 ∴DF=
∴DF=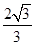
∴sin∠DFE=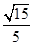
∴二面角 B-AC-D的正弦值是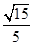 ………8分
………8分
(1)利用三视图可知△ABC为直角三角形,∠DBC为直角,AD⊥面DBC,DB=BC=1,AD=2,则DE的长为点D到面ABC的距离,以及三棱锥的体积可得。
(2)作DF⊥AC于点F,连结EF,
∵DE⊥面ABC ∴DE⊥AC ∴AC⊥面DEF ∴AC⊥EF
∴∠DFE是二面角 B-AC-D的平面角从而解三角形可知。
(1)

由三视图可得△ABC为直角三角形,∠DBC为直角,AD⊥面DBC,DB=BC=1,AD=2…………….2分
作DE⊥AB于点E
∵AD⊥面DBC,∴AD⊥BC
∵∠DBC为直角 ∴BC⊥面ADB
∴BC⊥DE
∴DE⊥面ABC………3分
∴DE的长为点D到面ABC的距离
∵DB=1,AD=2 ∴DE=
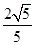 ∴点D到平面ABC的距离为
∴点D到平面ABC的距离为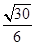 ………4分
………4分∵
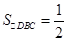 ,∴
,∴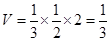 ………5分
………5分(2) 作DF⊥AC于点F,连结EF,
∵DE⊥面ABC ∴DE⊥AC ∴AC⊥面DEF ∴AC⊥EF
∴∠DFE是二面角 B-AC-D的平面角………7分
∵DB="BC=1" ∴DC=
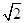 ∴DF=
∴DF=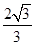
∴sin∠DFE=
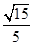
∴二面角 B-AC-D的正弦值是
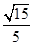 ………8分
………8分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
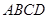 中,
中,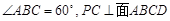 ,
,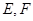 是
是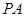 和
和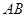 的中点.(Ⅰ)求证:
的中点.(Ⅰ)求证: 平面
平面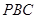 ;
;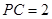 ,求
,求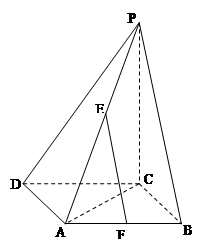
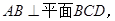 M、N分别是AC、AD的中点,BC
M、N分别是AC、AD的中点,BC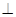 CD.
CD.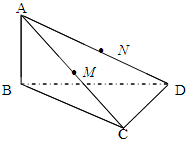
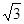 ,求直线AC与平面BCD所成的角.
,求直线AC与平面BCD所成的角. 的底面为菱形,且
的底面为菱形,且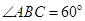 ,
,
 .
.
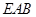
 平面
平面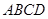 ;
; 的余弦值.
的余弦值.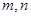 与平面
与平面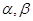 ,有以下四个命题:
,有以下四个命题: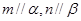 且
且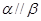 ,则
,则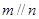 ;
;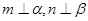 且
且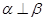 ,则
,则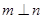 ;
;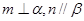 且
且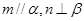 且
且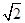 C.1 D.
C.1 D.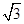
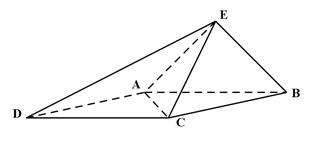
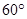 的菱形
的菱形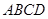 沿较短对角线
沿较短对角线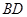 折成四面体
折成四面体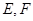 分别为
分别为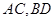 的中点,则下列命题中正确的是 。
的中点,则下列命题中正确的是 。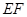 ∥
∥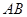 ;②
;②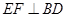 ;③
;③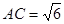 ; ⑤
; ⑤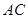 垂直于截面
垂直于截面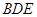 .
.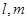 ,平面
,平面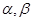 ,且
,且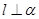 ,
,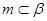 ,给出下列四个命题:
,给出下列四个命题: ∥
∥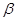 ,则
,则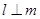 ;②若
;②若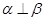 ,则
,则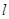 ∥
∥ ;④若
;④若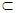 α,b
α,b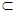 β α∥β
β α∥β