题目内容
已知正整数列{an}的前n项和为Sn,且对任意的正整数n满足2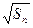 =an+1.
=an+1.
(1)求数列{an}的通项公式;
(2)设bn=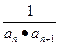 ,求数列{bn}的前n项和Bn.
,求数列{bn}的前n项和Bn.
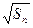 =an+1.
=an+1.(1)求数列{an}的通项公式;
(2)设bn=
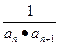 ,求数列{bn}的前n项和Bn.
,求数列{bn}的前n项和Bn.(1) 数列{an}是首项为1,公差为2的等差数列.
∴an=1+(n-1)×2=2n-1.
(2)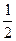 (1-
(1-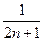 )=
)=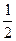 -
-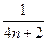 .
.
∴an=1+(n-1)×2=2n-1.
(2)
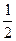 (1-
(1-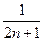 )=
)=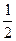 -
-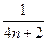 .
.(1)∵对任意的正整数n,2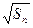 =an+1 ①
=an+1 ①
恒成立,
当n=1时,2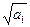 =a1+1,即(
=a1+1,即(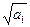 -1)2=0,
-1)2=0,
∴a1=1.
当n≥2时,有2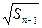 =an-1+1. ②
=an-1+1. ②
①2-②2得4an=an2-an-12+2an-2an-1,
即(an+an-1)(an-an-1-2)=0.∵an>0,∴an+an-1>0.∴an-an-1=2.
∴数列{an}是首项为1,公差为2的等差数列.
∴an=1+(n-1)×2=2n-1.
(2)∵an+1=2n+1,
∴bn=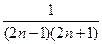 =
=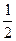 (
(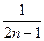 -
-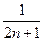 ).
).
∴Bn=b1+b2+b3+…+bn=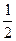 (1-
(1-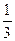 )+
)+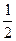 (
(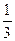 -
-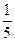 )+
)+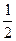 (
(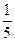 -
-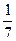 )+…+
)+…+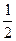 (
(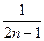 -
-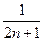 )
)
=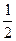 (1-
(1-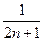 )=
)=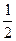 -
-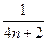 .
.
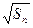 =an+1 ①
=an+1 ①恒成立,
当n=1时,2
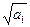 =a1+1,即(
=a1+1,即(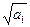 -1)2=0,
-1)2=0,∴a1=1.
当n≥2时,有2
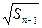 =an-1+1. ②
=an-1+1. ②①2-②2得4an=an2-an-12+2an-2an-1,
即(an+an-1)(an-an-1-2)=0.∵an>0,∴an+an-1>0.∴an-an-1=2.
∴数列{an}是首项为1,公差为2的等差数列.
∴an=1+(n-1)×2=2n-1.
(2)∵an+1=2n+1,
∴bn=
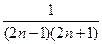 =
=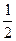 (
(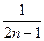 -
-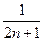 ).
).∴Bn=b1+b2+b3+…+bn=
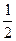 (1-
(1-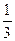 )+
)+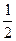 (
(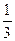 -
-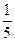 )+
)+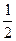 (
(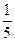 -
-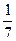 )+…+
)+…+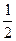 (
(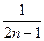 -
-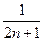 )
)=
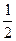 (1-
(1-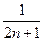 )=
)=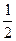 -
-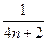 .
.
练习册系列答案
相关题目
 f(bn-1) (n∈N,n≥2),求证:
f(bn-1) (n∈N,n≥2),求证: 为等差数列,并求bn.
为等差数列,并求bn. 时,求Sn.
时,求Sn. 的等差数列,则a+b的值是________________.
的等差数列,则a+b的值是________________.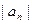 满足:
满足: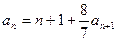 ,且存在大于1的整数k使
,且存在大于1的整数k使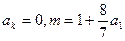 。
。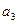 表示m(不必化简)
表示m(不必化简)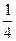 的等差数列,则a+b的值为( )
的等差数列,则a+b的值为( )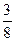
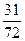
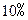 的速度增长,这个城市近10 年的国内生产总值一共是多少?
的速度增长,这个城市近10 年的国内生产总值一共是多少?