题目内容
【题目】【2018届江西省南昌市高三第一轮】已知![]() 分别为
分别为![]() 三个内角
三个内角![]() 的对边,且
的对边,且![]() .
.
(Ⅰ)求![]() ;
;
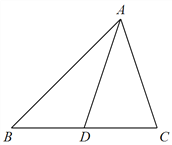
(Ⅱ)若![]() 为
为![]() 边上的中线,
边上的中线, ![]() ,
, ![]() ,求
,求![]() 的面积.
的面积.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析: (1)由正弦定理化简已知的式子,由内角和定理、诱导公式、两角和差的正弦公式化简后,由内角的范围和特殊角的三角函数值求出A;(2)由题意和平方关系求出sinB,由内角和定理、诱导公式、两角和的正弦公式求出sinC,由正弦定理求出a和c关系,根据题意和余弦定理列出方程,代入数据求出a、c,由三角形的面积公式求出答案.
解析:
(Ⅰ)∵![]() ,由正弦定理得:
,由正弦定理得:
![]() ,即
,即
![]() ,化简得:
,化简得: ![]() ,∴
,∴![]() .在
.在![]() 中,
中, ![]() ,∴
,∴![]() ,得
,得![]() .
.
(Ⅱ)在![]() 中,
中, ![]() ,得
,得![]() ,
,
则![]()
![]() ,由正弦定理得
,由正弦定理得![]() .
.
设![]() ,在
,在![]() 中,由余弦定理得:
中,由余弦定理得: ![]() ,
,
则![]() ,解得
,解得![]() ,即
,即![]() ,
,
故![]() .
.
点睛: 本题考查了正弦定理、余弦定理,三角形的面积公式,以及两角和差的正弦公式等,注意内角的范围,考查化简、变形、计算能力.注意当已知三角形的一个边和两个角时,用正弦定理.已知两角一对边时,用正弦定理,已知两边和对角时用正弦较多.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目