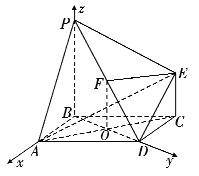
题目内容
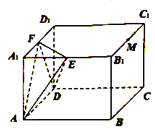
【题目】在如图所示的几何体中, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,在平行四边形
,在平行四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() .
.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
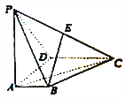
【解析】【试题分析】(1)连接![]() 交
交![]() 于
于![]() ,取
,取![]() 中点
中点![]() ,连接
,连接![]() ,
, ![]() ,利用中位线证明
,利用中位线证明![]() ,四边形
,四边形![]() 为平行四边形,从而
为平行四边形,从而![]() ,由此证得
,由此证得![]() 平面
平面![]() .(2)以
.(2)以![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 的方向为
的方向为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴的正方向建立空间直角坐标系,通过计算平面
轴的正方向建立空间直角坐标系,通过计算平面![]() 和平面
和平面![]() 的法向量来求二面角的余弦值.
的法向量来求二面角的余弦值.
【试题解析】
(1)证明:连接![]() 交
交![]() 于
于![]() ,取
,取![]() 中点
中点![]() ,连接
,连接![]() ,
, ![]() ,
,
因为![]() ,
, ![]() ,又
,又![]() ,
, ![]()
所以![]() ,
, ![]() ,从而
,从而![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)在平行四边形![]() 中,由于
中,由于![]() ,
, ![]() ,
, ![]() ,则
,则![]() ,又
,又![]() 平面
平面![]() ,则以
,则以![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 的方向为
的方向为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
则![]() ,
, ![]() ,
, ![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则由![]()
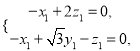
令![]() ,得
,得![]() ,
, ![]() ,所以
,所以![]() ,
,
![]() ,设平面
,设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则由![]() 即
即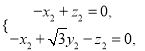
令![]() ,得
,得![]() ,
, ![]() ,所以
,所以![]() ,
,
![]() ,所以
,所以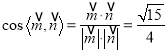 ,
,
所以所求二面角的余弦值为![]() .
.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目