题目内容
9.以抛物线x2=2my(m>0)的顶点O为圆心的圆,截该抛物线的准线所得的弦长为$\sqrt{3}$m(Ⅰ)求圆C的方程;
(Ⅱ)过圆C上任一点M作该圆的切线l,它与椭圆$\frac{x^2}{a}+\frac{y^2}{2}$=1(a∈R,且a>2)相交于A、B两点,当OA⊥OB时,求m的可能取值范围.
分析 (Ⅰ)由于圆C截抛物线的准线所得的弦长为$\sqrt{3}m$,所以圆C的半径$r=\sqrt{{{({\frac{m}{2}})}^2}+{{({\frac{{\sqrt{3}m}}{2}})}^2}}=m$,即可求圆C的方程;
(Ⅱ)分类讨论,利用OA⊥OB,x1x2+y1y2=0,得出m2=$\frac{2a}{a+2}$=2-$\frac{4}{a+2}$,即可求m的可能取值范围.
解答 解:(Ⅰ)已知抛物线的准线方程是$y=-\frac{m}{2}$(m>0),由于圆C截抛物线的准线所得的弦长为$\sqrt{3}m$,所以圆C的半径$r=\sqrt{{{({\frac{m}{2}})}^2}+{{({\frac{{\sqrt{3}m}}{2}})}^2}}=m$,故所求圆的方程是x2+y2=m2;
(Ⅱ)当圆C的切线l的斜率存在时,设方程为y=kx+t,A,B两点的坐标分别为(x1,y1),(x2,y2),
代入椭圆方程,可得(2+ak2)x2+2aktx+at2-2a=0,
∴x1+x2=-$\frac{2akt}{2+a{k}^{2}}$,x1x2=$\frac{a{t}^{2}-2a}{2+a{k}^{2}}$,
∵OA⊥OB,
∴x1x2+y1y2=0,
∴(1+k2)x1x2+kt(x1+x2)+t2=0,
∴(1+k2)×$\frac{a{t}^{2}-2a}{2+a{k}^{2}}$+kt×(-$\frac{2akt}{2+a{k}^{2}}$)+t2=0①
∵直线l是圆的切线,
∴m=$\frac{|t|}{\sqrt{1+{k}^{2}}}$,
∴t2=m2(1+k2),
代入①整理可得m2=$\frac{2a}{a+2}$=2-$\frac{4}{a+2}$,
∵a>2,∴△>0恒成立;
当圆C的切线l的斜率不存在时,由OA⊥OB,同样可得m2=$\frac{2a}{a+2}$=2-$\frac{4}{a+2}$,
∵a>2,∴1<m2<2,
∵m>0,
∴1<m<$\sqrt{2}$.
点评 本题考查圆的方程,考查直线与椭圆的位置关系,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案| A. | -6 | B. | 6 | C. | -3 | D. | 3 |
 已知抛物线x2=4y的焦点为F,过焦点F且不平行于x轴的动直线l交抛物线于A(x1,y1),B(x2,y2)两点,抛物线在A、B两点处的切线交于点M.
已知抛物线x2=4y的焦点为F,过焦点F且不平行于x轴的动直线l交抛物线于A(x1,y1),B(x2,y2)两点,抛物线在A、B两点处的切线交于点M. 如图:平面上两点P(0,1),Q(3,6),在直线y=x上取两点M,N,使$|MN|=\sqrt{2}$且使|PM|+|MN|+|NQ|的值取最小,则N的坐标为$(\frac{9}{4},\frac{9}{4})$.
如图:平面上两点P(0,1),Q(3,6),在直线y=x上取两点M,N,使$|MN|=\sqrt{2}$且使|PM|+|MN|+|NQ|的值取最小,则N的坐标为$(\frac{9}{4},\frac{9}{4})$.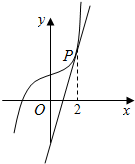 如图,已知函数f(x)=ax3+b,其图象上一点P处的切线为 l:y=4x-4,且点P的横坐标为2.
如图,已知函数f(x)=ax3+b,其图象上一点P处的切线为 l:y=4x-4,且点P的横坐标为2.