题目内容
20. 如图:平面上两点P(0,1),Q(3,6),在直线y=x上取两点M,N,使$|MN|=\sqrt{2}$且使|PM|+|MN|+|NQ|的值取最小,则N的坐标为$(\frac{9}{4},\frac{9}{4})$.
如图:平面上两点P(0,1),Q(3,6),在直线y=x上取两点M,N,使$|MN|=\sqrt{2}$且使|PM|+|MN|+|NQ|的值取最小,则N的坐标为$(\frac{9}{4},\frac{9}{4})$.
分析 求出P关于直线y=x的对称点,过Q(3,6)作平行于y=x的直线为y=x+3,将|PM|+|MN|+|NQ|的值进行转化求|P′M|+|MQ′|的最小值,利用数形结合以及根据两点间的距离公式进行求解即可
解答 解:P点关于直线y=x的对称点为P′(1,0),则有|PM|+|MN|+|NQ|=|P′M|+|MN|+|NQ|,
又过Q(3,6)作平行于y=x的直线为y=x+b;由6=3+b得b=3,即此时直线为y=x+3,
过M点作MQ′∥NQ,
则|MQ′|=|NQ|,|QQ′|=|MN|=$\sqrt{2}$;
则|P′M|+|MN|+|NQ|=|P′M|+|MN|+|MQ′|,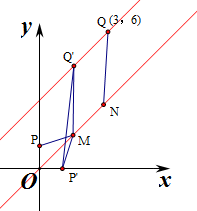
∵|MN|是常数,
∴要使|PM|+|MN|+|NQ|的值取最小,
则|P′M|+|MQ′|的值取最小,即P′,M,Q′三点共线时最小,
则设Q′(a,a+3),(a<3),由|QQ′|=|MN|=$\sqrt{2}$;
得$\sqrt{(a-3)^{2}+(6-a-3)^{2}}=\sqrt{2}$,即2(a-3)2=2,即(a-3)2=1,
∴a=4(舍)或a=2,即Q′(2,5),
设M(x,x),则x$\frac{x-0}{x-1}=\frac{5-0}{2-1}=5$,解得x=$\frac{5}{4}$,即M($\frac{5}{4}$,$\frac{5}{4}$),
设N(b,b),b>$\frac{5}{4}$,
由|MN|=$\sqrt{2}$;得$\sqrt{(b-\frac{5}{4})^{2}+(b-\frac{5}{4})^{2}}=\sqrt{2}$,
得2(b-$\frac{5}{4}$)2=2,即(b-$\frac{5}{4}$)=1,则b-$\frac{5}{4}$=1或b-$\frac{5}{4}$=-1,
即b=$\frac{9}{4}$或b=$\frac{1}{4}$(舍),故N($\frac{9}{4}$,$\frac{9}{4}$),
故答案为:($\frac{9}{4}$,$\frac{9}{4}$)
点评 本题主要考查两点间距离的应用,利用对称性将条件进行转化是解决本题的关键.综合性较强,难度较大.

 53随堂测系列答案
53随堂测系列答案| A. | 2 | B. | 1 | C. | 3 | D. | 4 |
| A. | (1,+∞) | B. | (-∞,3) | C. | [2,3) | D. | (1,3) |