题目内容
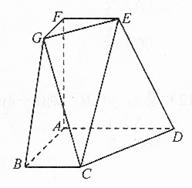
在如图所示的几何体中,四边形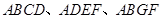 均为全等的直角梯形,且
均为全等的直角梯形,且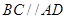 ,
,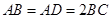 .
.
(Ⅰ)求证: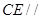 平面
平面 ;
;
(Ⅱ)设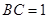 ,求点
,求点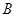 到平面
到平面 的距离.
的距离.
(Ⅰ)证明过程详见解析;(Ⅱ) .
.
解析试题分析:本题考查线面平行的判定以及二面角的求法.线面平行的判断:①判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;②性质:如果两个平面平行,其中一个平面内的直线必平行于另一个平面;③性质:如果两条平行线中的一条平行于一个平面,那么另一条也平行于这个平面或在这个平面内;④性质:如果一条直线平行于两个平行平面中的一个,那么这条直线也平行于另一个平面或在这个平面内;⑤性质:如果一个平面和平面外的一条直线都垂直于同一平面,那么这条直线和这个平面平行.第一问是利用线面平行的判定定理证明;第二问是求点到平面的距离,先通过线面平行将点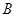 到面的距离转化为点
到面的距离转化为点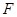 到面的距离,再利用等体积法求出几何体的高,也就是点
到面的距离,再利用等体积法求出几何体的高,也就是点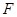 到面的距离.
到面的距离.
试题解析:(Ⅰ)连结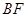 ,由题意,可知
,由题意,可知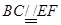 ,故四边形
,故四边形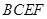 是平行四边形,所以
是平行四边形,所以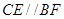 .
.
又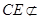 平面
平面 ,
,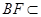 平面
平面 ,所以
,所以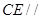 平面
平面 . 5分
. 5分
(Ⅱ)设点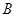 到平面
到平面 的距离为
的距离为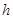 .
.
由(Ⅰ)知: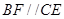 ,可得
,可得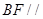 平面
平面 ,
,
故点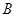 到平面
到平面 的距离等于点
的距离等于点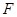 到平面
到平面 的距离,
的距离,
所以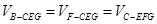 ,
,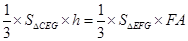 .
.
依题意,在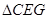 中,
中,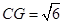 ,
,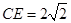 ,
,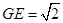 ,
,
因为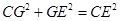 ,
,
所以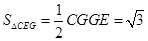 .
.
在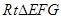 中,
中,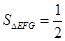 ,又
,又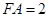 ,
,
故点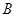 到平面
到平面 的距离为
的距离为 . 12分
. 12分
考点:1.线面平行的判定;2.等体积法解题.

练习册系列答案
相关题目
 , BD=BC=1, AA1=2,E为DC的中点,F是棱DD1上的动点.
, BD=BC=1, AA1=2,E为DC的中点,F是棱DD1上的动点.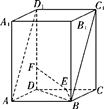
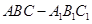 中,
中, ,
, ,
, 是
是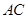 的中点.
的中点.
 平面
平面 ;
; 的余弦值.
的余弦值. 中,底面
中,底面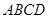 是正方形,侧面
是正方形,侧面 是正三角形,平面
是正三角形,平面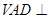 底面
底面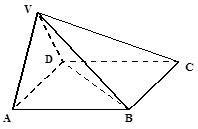
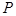 为线段VC的中点,求证:
为线段VC的中点,求证: 平面
平面 ;
; 的体积.
的体积.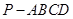 的底面为矩形,
的底面为矩形,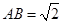 ,
,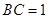 ,
, 分别是
分别是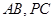 的中点,
的中点,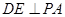 .
.
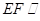 平面
平面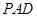 ;
;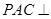 平面
平面 .
.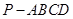 中,侧棱
中,侧棱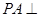 底面
底面 ,底面
,底面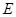 为
为 上一点,
上一点,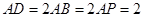 ,
,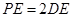 .
.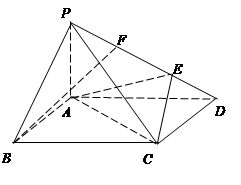
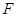 为
为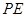 的中点,求证
的中点,求证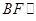 平面
平面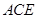 ;
; 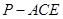 的体积.
的体积. 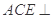 平面
平面 ,四边形
,四边形 .
.
 平面
平面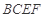 ;
;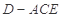 的体积.
的体积. 的边长为3,点
的边长为3,点 、
、 分别是边
分别是边 、
、 上的点,且满足
上的点,且满足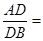
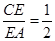 (如图1).将△
(如图1).将△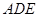 沿
沿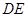 折起到△
折起到△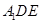 的位置,使二面角
的位置,使二面角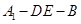 成直二面角,连结
成直二面角,连结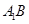 、
、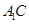 (如图2).
(如图2).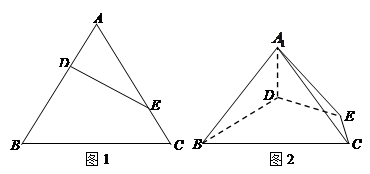
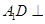 平面
平面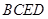 ;
; 上是否存在点
上是否存在点 ,使直线
,使直线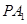 与平面
与平面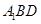 所成的角为
所成的角为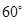 ?若存在,求出
?若存在,求出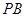 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.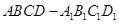 中,
中,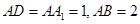 ,点E为AB的中点.
,点E为AB的中点.
 与平面
与平面 所成的角;
所成的角;  的平面角的正切值.
的平面角的正切值.