题目内容
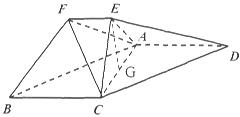
在如图所示的几何体中,平面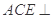 平面
平面 ,四边形
,四边形 为平行四边形,
为平行四边形, .
.
(Ⅰ)求证: 平面
平面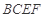 ;
;
(Ⅱ)求三棱锥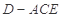 的体积.
的体积.
(I)详见解析;(II) .
.
解析试题分析:(I)利用两平面垂直的性质定理,证明BC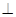 平面AEC,再根据线面垂直的性质定理证明AE
平面AEC,再根据线面垂直的性质定理证明AE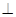 BC,根据勾股定理证明AE
BC,根据勾股定理证明AE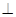 EC,利用线面垂直的判定定理证明AE
EC,利用线面垂直的判定定理证明AE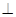 平面BCEF;(II)三棱锥体积利用体积转换为以E为顶点,
平面BCEF;(II)三棱锥体积利用体积转换为以E为顶点,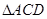 为底面的椎体体积求得.
为底面的椎体体积求得.
试题解析::(I)∵平面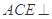 平面ABCD,且平面
平面ABCD,且平面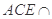 平面ABCD=AC,
平面ABCD=AC,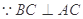
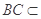 平面BCEF
平面BCEF 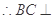 平面AEC ,
平面AEC , 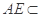 平面AEC
平面AEC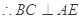 , 又
, 又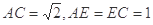

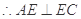 , 且
, 且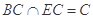 ,
,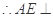 平面ECBF.
平面ECBF.
(II)设AC的中点为G,连接EG,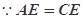 ,
, 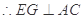 ,
,
∵平面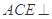 平面ABCD,且平面
平面ABCD,且平面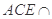 平面
平面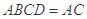 ,
,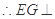 平面ABCD
平面ABCD 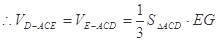
 ,
,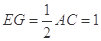 ,
,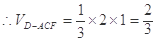 ,即三棱锥D-ACF的体积为
,即三棱锥D-ACF的体积为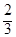 .
. 
考点:1、线面垂直的判定和性质定理应用;2、面面垂直的性质定理应用;3、用体积转换法求椎体体积.

练习册系列答案
相关题目
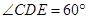 ,M是DE的中点,F是AC的中点,且AC=4,
,M是DE的中点,F是AC的中点,且AC=4,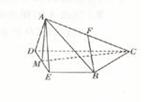
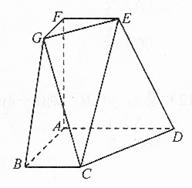
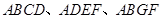 均为全等的直角梯形,且
均为全等的直角梯形,且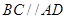 ,
,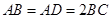 .
.
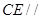 平面
平面 ;
;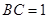 ,求点
,求点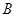 到平面
到平面 的距离.
的距离.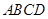 的边长为4,
的边长为4,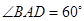 ,
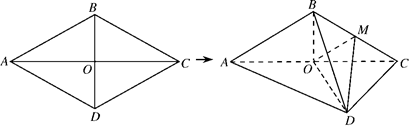
,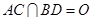 .将菱形
.将菱形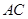 折起,得到三棱锥
折起,得到三棱锥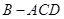 ,点
,点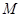 是棱
是棱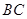 的中点,
的中点, .
.
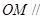 平面
平面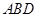 ;
;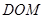
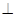 平面
平面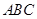 ;
;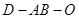 的余弦值.
的余弦值. 所在平面与直角梯形ABCD所在平面互相垂直,
所在平面与直角梯形ABCD所在平面互相垂直, ,
, 点
点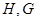 分别是线段
分别是线段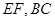 的中点.
的中点. 
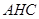
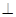 平面
平面 ;
;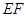 上是否存在点
上是否存在点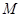 ,使得
,使得
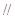 平面
平面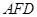 ,若存在,求
,若存在,求 的长并证明;若不存在,说明理由.
的长并证明;若不存在,说明理由.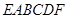 的底面
的底面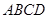 是边长为
是边长为 的正方形,
的正方形,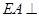 底面
底面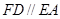 ,且
,且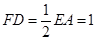 .
.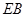 与平面
与平面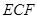 所成角的正弦值;
所成角的正弦值;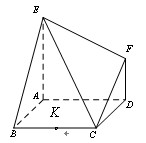
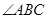 =
=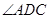 =90°
=90°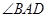 =1200,AD=AB=1,AC交BD于 O 点.
=1200,AD=AB=1,AC交BD于 O 点.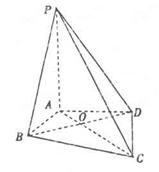
 是正方形,
是正方形,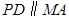 ,
,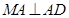 ,
,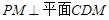 ,
, 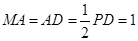
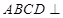 平面
平面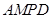 ;
; 的高
的高 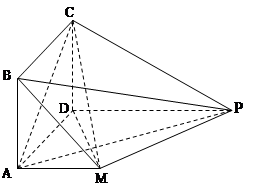
 是正方形,
是正方形, ⊥平面
⊥平面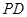 ∥
∥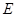 、
、 、
、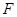 分别为
分别为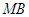 、
、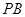 、
、 的中点,且
的中点,且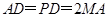 .
.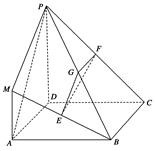
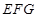 ⊥平面
⊥平面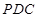 ;
;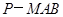 与四棱锥
与四棱锥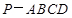 的体积之比.
的体积之比.