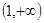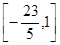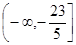题目内容
设二次函数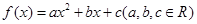 满足下列条件:
满足下列条件:
①当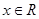 时,
时, 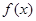 的最小值为0,且
的最小值为0,且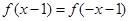 恒成立;
恒成立;
②当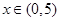 时,
时,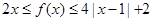 恒成立.
恒成立.
(I)求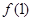 的值;
的值;
(Ⅱ)求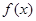 的解析式;
的解析式;
(Ⅲ)求最大的实数m(m>1),使得存在实数t,只要当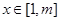 时,就有
时,就有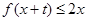 成立
成立
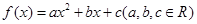 满足下列条件:
满足下列条件:①当
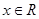 时,
时, 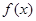 的最小值为0,且
的最小值为0,且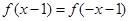 恒成立;
恒成立;②当
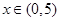 时,
时,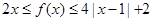 恒成立.
恒成立.(I)求
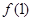 的值;
的值;(Ⅱ)求
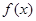 的解析式;
的解析式;(Ⅲ)求最大的实数m(m>1),使得存在实数t,只要当
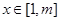 时,就有
时,就有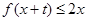 成立
成立(1) f(1)="2" ;(2) f(x)= 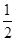 (x+1)2; (3) m的最大值为9.
(x+1)2; (3) m的最大值为9.
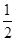 (x+1)2; (3) m的最大值为9.
(x+1)2; (3) m的最大值为9. 试题分析:(1)在②中令x=1,有2≤f(1)≤2,故f(1)="2"
(2)由①知二次函数的关于直线x=-1对称,且开口向上
故设此二次函数为f(x)=a(x+1)2,(a>0),∵f(1)=2,∴a=
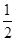
∴f(x)=
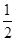 (x+1)2
(x+1)2(3)假设存在t∈R,只需x∈[1,m],就有f(x+t)≤2x.
f(x+t)≤2x
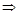
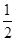 (x+t+1)2≤2x
(x+t+1)2≤2x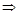 x2+(2t-2)x+t2+2t+1≤0.
x2+(2t-2)x+t2+2t+1≤0.令g(x)=x2+(2t-2)x+t2+2t+1,g(x)≤0,x∈[1,m].
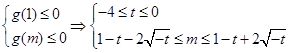
∴m≤1-t+2
 ≤1-(-4)+2
≤1-(-4)+2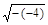 =9
=9t=-4时,对任意的x∈[1,9]
恒有g(x)≤0, ∴m的最大值为9.(画图用数形结合视解答情况给分)
点评:典型题,本题综合考查“二次问题”,运用了从特殊到一般的思想方法。(3)作为存在性问题,转化成一个二次不等式在给定闭区间恒成立问题,借助于函数单调性,通过限制区间端点函数值的范围,得到不等式组,使问题得解。

练习册系列答案
相关题目
 的图象顶点为
的图象顶点为 ,且图象在
,且图象在 轴上截得线段长为8,则函数
轴上截得线段长为8,则函数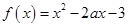 在区间
在区间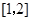 上是单调函数的条件是( )
上是单调函数的条件是( )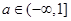
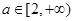
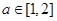

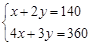
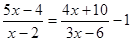
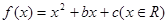 ,且
,且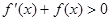 恒成立,则对
恒成立,则对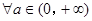 ,下面不等式恒成立的是( )
,下面不等式恒成立的是( )



 的解集为
的解集为 ,则实数
,则实数 的取值范围是 。
的取值范围是 。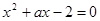 在区间
在区间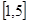 上有解,则实数
上有解,则实数 的取值范围是 ( )
的取值范围是 ( )