题目内容
函数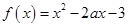 在区间
在区间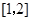 上是单调函数的条件是( )
上是单调函数的条件是( )
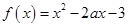 在区间
在区间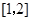 上是单调函数的条件是( )
上是单调函数的条件是( )A.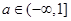 | B.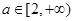 |
C.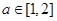 | D. |
D
试题分析:为保证函数
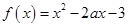 在区间
在区间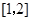 上是单调函数,[1,2]应是二次函数单调区间的子区间,即[1,2]在二次函数对称轴
上是单调函数,[1,2]应是二次函数单调区间的子区间,即[1,2]在二次函数对称轴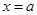 的一侧,
的一侧,所以,
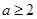 或
或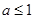 ,故选D。
,故选D。点评:简单题,涉及二次函数问题,往往结合二次函数的开口方向、对称轴位置加以思考。

练习册系列答案
相关题目
题目内容
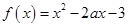 在区间
在区间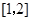 上是单调函数的条件是( )
上是单调函数的条件是( )A.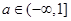 | B.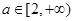 |
C.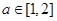 | D. |
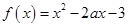 在区间
在区间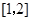 上是单调函数,[1,2]应是二次函数单调区间的子区间,即[1,2]在二次函数对称轴
上是单调函数,[1,2]应是二次函数单调区间的子区间,即[1,2]在二次函数对称轴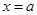 的一侧,
的一侧,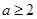 或
或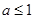 ,故选D。
,故选D。