题目内容
一次函数f(x)是减函数,且满足f[f(x)]=4x-1,则f(x)=__________.
-2x+1
试题分析:由一次函数f(x)是减函数,可设f(x)=kx+b(k<0).
则f[f(x)]=kf(x)+b=k(kx+b)+b=k2x+kb+b,
∵f[f(x)]=4x-1,
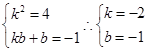
∴f(x)=-2x+1.
点评:对于解析式的求解很多时候待定系数法是常用方法之一,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
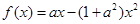 ,其中
,其中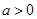 ,区间
,区间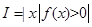
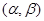 的长度定义为
的长度定义为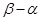 );
);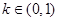 ,当时,求长度的最小值.
,当时,求长度的最小值.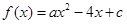 的值域为
的值域为 ,则
,则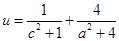 的最小值为 .
的最小值为 .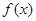 的最小值为1,且
的最小值为1,且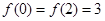 .
.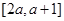 上不单调,求实数
上不单调,求实数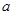 的取值范围;
的取值范围;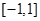 上,
上,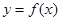 的图像恒在
的图像恒在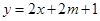 的图像上方,试确定实数
的图像上方,试确定实数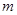 的取值范围.
的取值范围.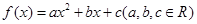 满足下列条件:
满足下列条件: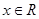 时,
时, 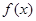 的最小值为0,且
的最小值为0,且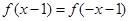 恒成立;
恒成立;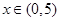 时,
时,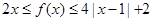 恒成立.
恒成立.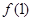 的值;
的值;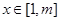 时,就有
时,就有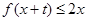 成立
成立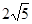 ,求实数m的取值范围.
,求实数m的取值范围.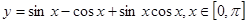 的值域是 .
的值域是 . 是方程
是方程 的两个实根,则
的两个实根,则 的最小值是
的最小值是

