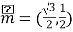题目内容
【题目】已知数列![]() 的通项公式为
的通项公式为![]() ,其中
,其中![]() ,
,![]() 、
、![]() .
.
(1)试写出一组![]() 、
、![]() 的值,使得数列
的值,使得数列![]() 中的各项均为正数.
中的各项均为正数.
(2)若![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() ,且对任意的
,且对任意的![]() (
(![]() ),均有
),均有![]() ,写出所有满足条件的
,写出所有满足条件的![]() 的值.
的值.
(3)若![]() ,数列
,数列![]() 满足
满足![]() ,其前
,其前![]() 项和为
项和为![]() ,且使
,且使![]() (
(![]() 、
、![]() ,
,![]() )的
)的![]() 和
和![]() 有且仅有
有且仅有![]() 组,
组,![]() 、
、![]() 、…、
、…、![]() 中有至少
中有至少![]() 个连续项的值相等,其它项的值均不相等,求
个连续项的值相等,其它项的值均不相等,求![]() 、
、![]() 的最小值.
的最小值.
【答案】(1) ![]() 、
、![]() (答案不唯一).(2) 7,8,9,10,11.(3)
(答案不唯一).(2) 7,8,9,10,11.(3) ![]() 的最小值为
的最小值为![]() .
.![]() 的最小值为
的最小值为![]()
【解析】
(1)只要![]() 均小于1即可;
均小于1即可;
(2)利用对勾函数![]() 的单调性分类讨论,注意
的单调性分类讨论,注意![]() 的取值只能是正整数.
的取值只能是正整数.
(3)![]() ,且
,且![]() ,求出
,求出
因为![]() ,只有四组
,只有四组![]() ,利用二次函数的性质得
,利用二次函数的性质得![]() ,进一步得
,进一步得![]() ,
,![]() 的四个值为
的四个值为![]() ,
,![]() ,
,![]() ,
,![]() ,因此,
,因此,![]() 的最小值为
的最小值为![]() .再由
.再由![]() 中有至少
中有至少![]() 个连续项的值相等,其它项的值均不相等,则
个连续项的值相等,其它项的值均不相等,则![]() 中接着至少有两个0,从而可得
中接着至少有两个0,从而可得![]() 的最小值.
的最小值.
(1)![]() 、
、![]() (答案不唯一).
(答案不唯一).
(2)由题设,![]() .
.
当![]() ,
,![]() 单调递增,不合题意,
单调递增,不合题意,
![]() 时,
时,![]() ,
,![]() 在
在![]() 时单调递增,不合题意,因此,
时单调递增,不合题意,因此,![]() .
.
当![]() 时,对于
时,对于![]() ,当
,当![]() 时,
时,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() 单调递增.
单调递增.
由题设,有![]() ,
,![]() .
.
于是由![]() 及
及![]() ,可解得
,可解得![]() .
.
因此,![]() 的值为7,8,9,10,11.
的值为7,8,9,10,11.
(3)因为![]() ,且
,且![]() ,
,
所以
因为![]() (
(![]() 、
、![]() ,
,![]() ),所以
),所以![]() 、
、![]() .
.
于是由![]() ,可得
,可得![]() ,进一步得
,进一步得![]() ,
,
此时,![]() 的四个值为
的四个值为![]() ,
,![]() ,
,![]() ,
,![]() ,因此,
,因此,![]() 的最小值为
的最小值为![]() .
.
又![]() 、
、![]() 、…、
、…、![]() 中有至少
中有至少![]() 个连续项的值相等,其它项的值均不相等,不妨设
个连续项的值相等,其它项的值均不相等,不妨设![]() ,于是有
,于是有![]() ,因为当
,因为当![]() 时,
时,![]() ,所以
,所以![]() ,
,
因此,![]() ,即
,即![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目