题目内容
(本题满分为10分)
在四面体ABCD中作截面PQR,若PQ,CB的延长线交于M;RQ,DB的延长线交于N;RP,DC的延长线交于K,求证:M、N、K三点共线.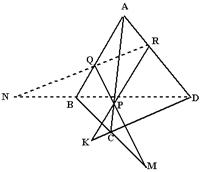
证明:M、N、K都同时在面ABC和面PQR内,所以在两面的交线上,所以三点共线
解析试题分析:由已知得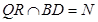 ,所以N在面ABC和面PQR内;
,所以N在面ABC和面PQR内;
同理K在面ABC和面PQR内;M在面ABC和面PQR内。
所以M、N、K应在面ABC和面PQR的交线上,即证得
M、N、K三点共线
考点:利用公理3证明三点共线
点评:公理3还可证明三线共点,做两面交线

练习册系列答案
相关题目
 平面CC1D1D,且PC=PD=
平面CC1D1D,且PC=PD= .
.
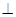 平面PBC;
平面PBC; ,当a为何值时,PC//平面
,当a为何值时,PC//平面 .
. ,底面
,底面 是正方形,
是正方形, 面
面 是
是 的中点,点
的中点,点 是
是 的中点,连接
的中点,连接 ,
,
 .
.
 面
面 ;
; ,
, ,求二面角
,求二面角 的余弦值.
的余弦值. ABC=60
ABC=60 ,EC
,EC 面ABCD,FA
面ABCD,FA
 中,
中,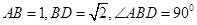 ,将它们沿对角线
,将它们沿对角线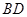 折起,折后的点
折起,折后的点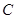 变为
变为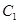 ,且
,且 .
.
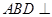 平面
平面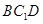 ;
;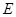 为线段
为线段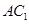 上的一个动点,当线段
上的一个动点,当线段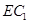 的长为多少时,
的长为多少时, 与平面
与平面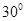 ?
?
 中,
中, 为正方形,
为正方形,
 分别是线段
分别是线段 的中点. 求证:
的中点. 求证: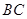 //平面
//平面 ;
;  .
.
 中,
中, 平面
平面 ,
, ,
, ,
, .
. ;
; 的正弦值;
的正弦值; 为棱
为棱 上的点,满足异面直线
上的点,满足异面直线 与
与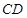 所成的角为
所成的角为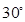 ,求
,求 的长.
的长.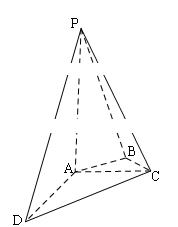
 ∩平面
∩平面 =AB,PQ⊥
=AB,PQ⊥