题目内容
【题目】在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在下面问题中,若问题中的正整数k存在,求k的值;若k不存在,请说明理由.
这三个条件中任选一个,补充在下面问题中,若问题中的正整数k存在,求k的值;若k不存在,请说明理由.
设![]() 为等差数列
为等差数列![]() 的前n项和,
的前n项和,![]() 是等比数列,______,
是等比数列,______,![]() ,
,![]() ,
,![]() .是否存在k,使得
.是否存在k,使得![]() 且
且![]() ?
?
【答案】方案①:存在![]() 满足题意;
满足题意;
方案②:存在![]() 满足题意;
满足题意;
方案③:存在![]() 满足题意.
满足题意.
【解析】
方案①②③解题思路均为如下思路:根据等比数列通项公式可求得![]() ,进而得到
,进而得到![]() ;根据两数列中的项的等量关系和等差数列通项公式可求得
;根据两数列中的项的等量关系和等差数列通项公式可求得![]() ,将结论变为
,将结论变为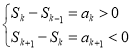 ,从而构造出不等式,结合
,从而构造出不等式,结合![]() 为正整数即可求得结果;
为正整数即可求得结果;
方案①
设等比数列![]() 的公比为
的公比为![]() ,等差数列
,等差数列![]() 的公差
的公差![]() ,
,
由![]() ,
,![]() 得:
得:![]() ,
,
又![]() ,∴
,∴![]() ,故
,故![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
由![]() 且
且![]() 可得:
可得: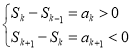 ,即
,即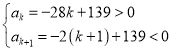 ,
,
解得:![]() ,又
,又![]() 为正整数,
为正整数,![]() ,
,
![]() 存在
存在![]() ,使得
,使得![]() 且
且![]() .
.
方案②
设等比数列![]() 的公比为
的公比为![]() ,等差数列
,等差数列![]() 的公差
的公差![]() ,
,
由![]() ,
,![]() 得:
得:![]() ,
,
又![]() ,∴
,∴![]() ,故
,故![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
由![]() 且
且![]() 可得:
可得: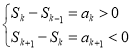 ,即
,即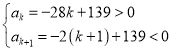 ,
,
解得:![]() ,又
,又![]() 为正整数,
为正整数,![]() ,
,
![]() 存在
存在![]() ,使得
,使得![]() 且
且![]() .
.
方案③
设等比数列![]() 的公比为
的公比为![]() ,等差数列
,等差数列![]() 的公差
的公差![]() ,
,
由![]() ,
,![]() 得:
得:![]() ,
,
又![]() ,∴
,∴![]() ,故
,故![]() ,
,
又![]() ,
,![]() ,即
,即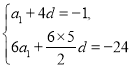 ,解得:
,解得:![]() ,
,
![]() .
.
由![]() 且
且![]() 可得:
可得: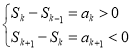 ,即
,即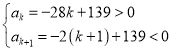 ,
,
解得:![]() ,又
,又![]() 为正整数,
为正整数,![]() ,
,
![]() 存在
存在![]() ,使得
,使得![]() 且
且![]() .
.

练习册系列答案
相关题目