题目内容
(本题满分15分)已知函数 .
.
(Ⅰ)若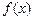 为定义域上的单调函数,求实数m的取值范围;
为定义域上的单调函数,求实数m的取值范围;
(Ⅱ)当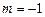 时,求函数
时,求函数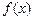 的最大值;
的最大值;
(Ⅲ)当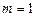 ,且
,且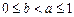 时,证明:
时,证明: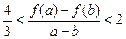 .
.
解: (Ⅰ) ,
,
∴ ---------2分
---------2分
若f(x)在 上是增函数,则
上是增函数,则 ,即
,即 在
在 恒成立,
恒成立,
而 ,故m≥0;-----------------------------------------2分
,故m≥0;-----------------------------------------2分
若f(x)在 上是减函数,则
上是减函数,则 ,即
,即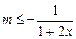 在
在 恒成立,
恒成立,
而 ,故这样的m不存在.------------------------------1分
,故这样的m不存在.------------------------------1分
经检验,当m≥0时, 对
对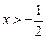 恒成立,
恒成立,
∴当m≥0时,f(x)在定义域上是单调增函数.---------------------1分
(Ⅱ)当m =-1时,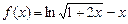 ,则
,则 ----------1分
----------1分
当 时,
时, ,此时f(x)为增函数,
,此时f(x)为增函数,
当 时,
时, ,此时f(x)为减函数----------------------------2分
,此时f(x)为减函数----------------------------2分
∴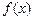 在x = 0时取得最大值,最大值为
在x = 0时取得最大值,最大值为 ----------------------1分
----------------------1分
(Ⅲ)当m = 1时,令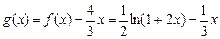 ,
,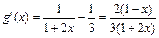 --1分
--1分
在[0,1]上总有 ,即
,即 在[0,1]上递增------------------------------1分
在[0,1]上递增------------------------------1分
∴当 时,
时,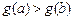 ,即
,即 ----1分
----1分
令 ,由(Ⅱ)知它在[0,1]上递减,所以当
,由(Ⅱ)知它在[0,1]上递减,所以当 时,
时,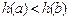 ,即
,即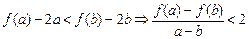 -----------------1分
-----------------1分
综上所述,当m = 1,且 时,
时, ---------------1分
---------------1分
解析

练习册系列答案
相关题目
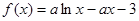 ,
,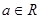
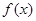 的单调区间。
的单调区间。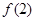 )处的切线的倾斜角为
)处的切线的倾斜角为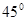 ,对任意的
,对任意的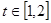 ,函数
,函数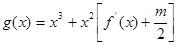 在区间
在区间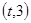 上总不是单调函数,求m取值范围
上总不是单调函数,求m取值范围
 ,
, .
. 的单调区间和最小值;
的单调区间和最小值; 的大小关系;
的大小关系;
 的取值范围,使得
的取值范围,使得 <
< 对任意
对任意 >0成立
>0成立 ,其中
,其中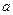 为常数.
为常数. ,
, 的图象恒过定点;
的图象恒过定点; 时,判断函数
时,判断函数 时,
时, 的最大值.
的最大值. 在
在 上是增函数,在
上是增函数,在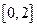 上是减函数,且方程
上是减函数,且方程 有三个根,它们分别是
有三个根,它们分别是 .
.  的值; (2)求证:
的值; (2)求证:  (3)求
(3)求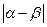 的取值范围.
的取值范围. .
. ,
,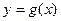 在
在 处的切线相互垂直,求这两个切线方程;
处的切线相互垂直,求这两个切线方程; 单调递增,求
单调递增,求 的取值范围.
的取值范围.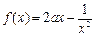 ,
, .
.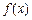 在
在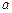 的取值范围;
的取值范围;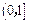 上的最大值.
上的最大值.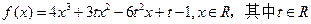 ,
,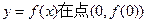 处的切线方程;
处的切线方程;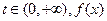 在区间(0,1)内均存在零点。
在区间(0,1)内均存在零点。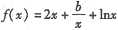 的一个极值点
的一个极值点 ,试问过点(2,5)可作多少条直线与曲线
,试问过点(2,5)可作多少条直线与曲线 相切?请说明理由.
相切?请说明理由.