题目内容
(本小题满分14分)
设函数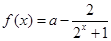 ,
,
(1)求证:不论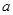 为何实数
为何实数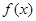 在定义域上总为增函数;
在定义域上总为增函数;
(2)确定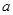 的值,使
的值,使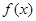 为奇函数;
为奇函数;
(3)当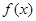 为奇函数时,求
为奇函数时,求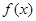 的值域.
的值域.
设函数
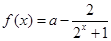 ,
,(1)求证:不论
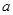 为何实数
为何实数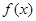 在定义域上总为增函数;
在定义域上总为增函数;(2)确定
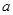 的值,使
的值,使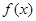 为奇函数;
为奇函数;(3)当
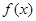 为奇函数时,求
为奇函数时,求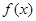 的值域.
的值域.(1) 见解析; (2) 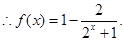
(3)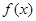 为奇函数时,其值域为
为奇函数时,其值域为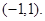
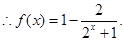
(3)
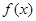 为奇函数时,其值域为
为奇函数时,其值域为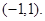
(1)先设x1<x2,欲证明不论a为何实数f(x)总是为增函数,只须证明:f(x1)-f(x2)<0,即可;
(2)根据f(x)为奇函数,利用定义得出f(-x)=-f(x)恒成立,从而求得a值即可.
(3)由(2)知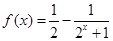 ,利用指数函数y=2x的性质结合不等式的性质即可求得f(x)的值域.
,利用指数函数y=2x的性质结合不等式的性质即可求得f(x)的值域.
(1)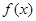 的定义域为R, 设
的定义域为R, 设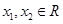 ,且
,且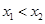 ,
,
则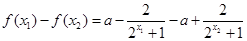 =
=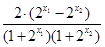 ,
,
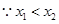 ,
, 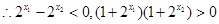 ,
,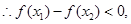
即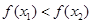 ,所以不论
,所以不论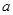 为何实数
为何实数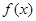 总为增函数.……………………5分
总为增函数.……………………5分
(2)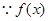 为奇函数,
为奇函数,  ,即
,即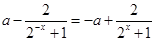 ,
,
整理得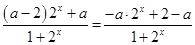 ,
,
则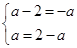 ,解得:
,解得: 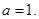
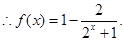 ……………………10分
……………………10分
(4)由(2)知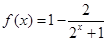 ,
,
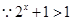 ,
,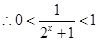 ,
,
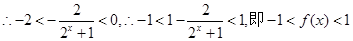
故当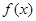 为奇函数时,其值域为
为奇函数时,其值域为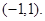 ……………………14分
……………………14分
另解:由(2)知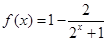 .
.
由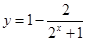 ,得
,得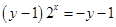 ,
,
当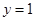 时,得
时,得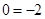 ,矛盾,所以
,矛盾,所以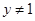 ;
;
故有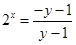 .
.
当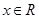 时,
时,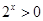 ,所以
,所以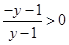 ,解得
,解得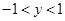 .
.
故当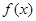 为奇函数时,其值域为
为奇函数时,其值域为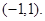 ………………14分
………………14分
(2)根据f(x)为奇函数,利用定义得出f(-x)=-f(x)恒成立,从而求得a值即可.
(3)由(2)知
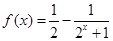 ,利用指数函数y=2x的性质结合不等式的性质即可求得f(x)的值域.
,利用指数函数y=2x的性质结合不等式的性质即可求得f(x)的值域.(1)
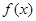 的定义域为R, 设
的定义域为R, 设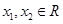 ,且
,且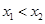 ,
,则
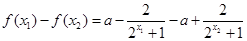 =
=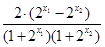 ,
,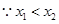 ,
, 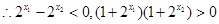 ,
,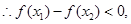
即
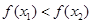 ,所以不论
,所以不论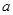 为何实数
为何实数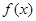 总为增函数.……………………5分
总为增函数.……………………5分(2)
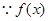 为奇函数,
为奇函数,  ,即
,即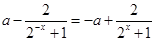 ,
,整理得
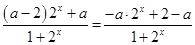 ,
,则
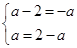 ,解得:
,解得: 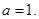
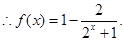 ……………………10分
……………………10分(4)由(2)知
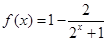 ,
, 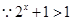 ,
,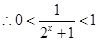 ,
,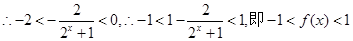
故当
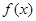 为奇函数时,其值域为
为奇函数时,其值域为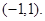 ……………………14分
……………………14分另解:由(2)知
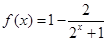 .
.由
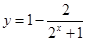 ,得
,得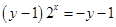 ,
,当
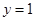 时,得
时,得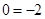 ,矛盾,所以
,矛盾,所以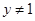 ;
;故有
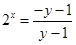 .
.当
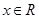 时,
时,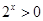 ,所以
,所以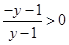 ,解得
,解得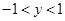 .
.故当
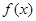 为奇函数时,其值域为
为奇函数时,其值域为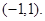 ………………14分
………………14分
练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目

 .
.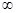 )上的函数,
)上的函数,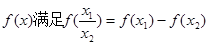 ,且当
,且当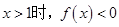 .① 求
.① 求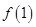 的值;② 判断
的值;② 判断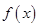 的单调性;③ 若
的单调性;③ 若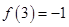 ,解不等式
,解不等式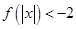 .
.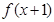 的定义域为[0,1],则
的定义域为[0,1],则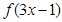 的定义域为 .
的定义域为 .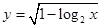 的定义域为 ( )
的定义域为 ( )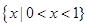
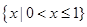

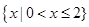
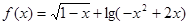 的定义域为_________
的定义域为_________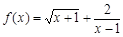 的定义域是 ..
的定义域是 ..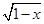 +
+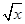 的定义域为( )
的定义域为( ) 的值域为
的值域为