题目内容

【题目】已知是定义在上的奇函数，且时， ，则函数（为自然对数的底数）的零点个数是（ ）

A. 0 B. 1 C. 2 D. 3

【答案】C

【解析】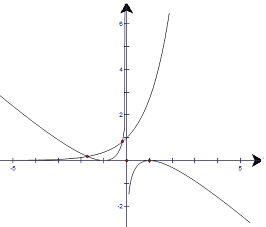

当时,函数求导可得,则函数在上单调递增,在上单调递减,当时函数有极大值为 ,根据奇函数的对称性,作出其函数图像如图,由函数图像可知与有两个不同交点,则 有两个零点.故本题选.

点睛:本题主要考查函数的奇偶性,单调性,指数函数的图像与性质,及数形结合的数学思想方法.函数的零点问题,方程解的个数问题一般转化为两个常见的函数图像的交点个数问题来解决.要能熟练掌握几种基本函数图像,如二次函数,反比例函数,指数函数,对数函数,幂函数等.掌握平移变换,伸缩变换,对称变换,翻折变换,周期变换等常用的方法技巧来快速处理图像.能利用函数的相关性质作出函数的草图.

练习册系列答案
相关题目

【题目】已知函数f（x）=+x在x=1处的切线方程为2x﹣y+b=0．

（Ⅰ）求实数a，b的值；

（Ⅱ）若函数g（x）=f（x）+x2﹣kx，且g（x）是其定义域上的增函数，求实数k的取值范围．

【题目】已知两圆C1：x2＋y2－2x－6y－1＝0和C2：x2＋y2－10x－12y＋45＝0.

(1)求证：圆C1和圆C2相交；

(2)求圆C1和圆C2的公共弦所在直线的方程和公共弦长．

【题目】设函数， ，且函数的图象关于直线对称。

(1)求函数在区间上最大值；

(2)设，不等式在上恒成立，求实数的取值范围；

(3)设有唯一零点，求实数的值。

【题目】下列说法：

①将一组数据中的每个数据都加上或减去同一个常数后，均值与方差都不变；

②设有一个回归方程，变量x增加一个单位时，y平均增加3个单位；

③线性回归方程必经过点；

④在吸烟与患肺病这两个分类变量的计算中，从独立性检验知，有99％的把握认为吸烟与患肺病有关系时，我们说现有100人吸烟，那么其中有99人患肺病．其中错误的个数是（ ）

A. 0

B. 1

C. 2

D. 3

【题目】已知函数f(x)＝x2－2|x|－1，－3≤x≤3.

(1)证明：f(x)是偶函数；

(2)指出函数f(x)的单调区间；

(3)求函数的值域.

【题目】已知函数f(x)＝x2－1，g(x)＝

(1)求f[g(2)]和g[f(2)]的值；

(2)求f[g(x)]和g[f(x)]的表达式．

【题目】（本小题满分12分）

甲乙两个班级进行一门课程的考试，按照学生考试成绩优秀和不优秀统计成绩后，得到如下的列联表：

班级与成绩列联表

优 秀

不优秀

甲 班

10

35

乙 班

7

38

根据列联表的独立性检验，能否在犯错误的概率不超过0.01的前提下认为成绩与班级有关系？

附：

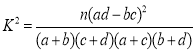
0.50

0.40

0.25

0.15

0.10

0.05

0.025

0.010

0.005

0.001

0.455

0.708

1.323

2.072

2.706

3.841

5.024

6.635

7.879

10.828

【题目】已知函数，其中是自然对数的底数.

（1）证明是上的偶函数

（2）若关于的不等式在上恒成立，求实数的取值范围.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网