题目内容
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,底面ABC等边三角形,E,F分别是BC,CC1的中点.求证: (Ⅰ) EF∥平面A1BC1;
(Ⅱ) 平面AEF⊥平面BCC1B1 . 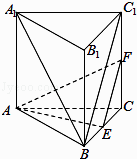
【答案】证明:(Ⅰ)因为E,F分别是BC,CC1的中点, 所以EF∥BC1 .
又因为BC1平面A1BC1 , EF平面A1BC1 ,
所以EF∥平面A1BC1 . (6分)
(Ⅱ)因为三棱柱ABC﹣A1B1C1是直三棱柱,
所以BB1⊥平面ABC.又AE平面ABC,
所以AE⊥BB1 .
又因为△ABC为正三角形,E为BC的中点,
所以AE⊥BC.
又BB1∩BC=B,所以AE⊥平面BCC1B1 .
又AE平面AEF,所以平面AEF⊥平面BCC1B1 . 
【解析】(Ⅰ)由三角形中位线定理得EF∥BC1 , 由此能证明EF∥平面A1BC1 . (Ⅱ)由三棱柱ABC﹣A1B1C1是直三棱柱,得AE⊥BB1 , 由正三角形性质得AE⊥BC,由此能证明平面AEF⊥平面BCC1B1 .
【考点精析】通过灵活运用直线与平面平行的判定和平面与平面垂直的判定,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直即可以解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目