题目内容
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60° 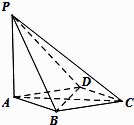
(1)若PA=AB,求PB与平面PDC所成角的正弦值;
(2)当平面PBC与平面PDC垂直时,求PA的长.
【答案】
(1)解:设AC∩BD=O,∵在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,PA=AB=2,∠BAD=60°
∴BO=1,AO=CO= ![]() ,
,
如图,以O为坐标原点,建立空间直角坐标系O﹣xyz,
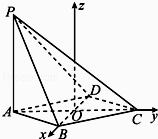
则 P(0,﹣ ![]() ,2),A(0,﹣
,2),A(0,﹣ ![]() ,0),B(1,0,0),C(0,
,0),B(1,0,0),C(0, ![]() ,0),D(﹣1,0,0)
,0),D(﹣1,0,0)
∴ ![]() =(1,
=(1, ![]() ,﹣2),
,﹣2), ![]() =(﹣1,
=(﹣1, ![]() ,﹣2),
,﹣2), ![]() =(0,2
=(0,2 ![]() ,﹣2),
,﹣2),
设平面PDC的法向量 ![]() =(x,y,z),
=(x,y,z),
则 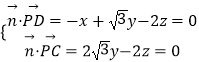 ,取y=
,取y= ![]() ,得
,得 ![]() =(﹣3,
=(﹣3, ![]() ,3),
,3),
设PB与平面PDC所成角为θ,
则sinθ ![]() =
= ![]() =
= ![]() .
.
∴PB与平面PDC所成角的正弦值为 ![]()
(2)解:由(1)知 ![]() =(﹣1,
=(﹣1, ![]() ,0),设P(0,﹣
,0),设P(0,﹣ ![]() ,t)(t>0),
,t)(t>0),
则 ![]() =(﹣1,﹣
=(﹣1,﹣ ![]() ,t),设平面PBC的法向量
,t),设平面PBC的法向量 ![]() =(x,y,z),
=(x,y,z),
则  ,取y=
,取y= ![]() ,得
,得 ![]() =(3,
=(3, ![]() ,
, ![]() ),
),
同理,平面PDC的法向量 ![]() =(﹣3,
=(﹣3, ![]() ,
, ![]() ),
),
∵平面PCB⊥平面PDC,∴ ![]() =﹣9+3+
=﹣9+3+ ![]() =0,
=0,
解得t= ![]() ,∴PA=
,∴PA= ![]() .
.
【解析】(1)设AC∩BD=O,以O为坐标原点,建立空间直角坐标系O﹣xyz,利用向量法能求出PB与平面PDC所成角的正弦值.(2)求出平面PBC的法向量和平面PDC的法向量,利用向量法能求出PA的长.
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直,以及对空间角的异面直线所成的角的理解,了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则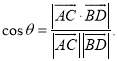 .
.

【题目】某校为了解高三年级不同性别的学生对取消艺术课的态度(支持或反对),进行了如下的调查研究.全年级共有1350人,男女生比例为8:7,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为 ![]() ,通过对被抽取学生的问卷调查,得到如下2x2列联表:
,通过对被抽取学生的问卷调查,得到如下2x2列联表:
支持 | 反对 | 总计 | |
男生 | 30 | ||
女生 | 25 | ||
总计 |
(Ⅰ)完成列联表,并判断能否有99.9%的把握认为态度与性别有关?
(Ⅱ)若某班有6名男生被抽到,其中2人支持,4人反对;有4名女生被抽到,其中2人支持,2人反对,现从这10人中随机抽取一男一女进一步调查原因.求其中恰有一人支持一人反对的概率.
参考公式及临界表:K2= ![]()
P(K2≥k0) | 0.10 | 0.050 | 0.010 | 0.005 | 0.001 |
k0 | 2.706% | 3.841 | 6.635 | 7.879 | 10.828 |