题目内容
设数列{an}的前n项和为Sn,a1=1,且对任意正整数n,点(an+1,Sn)在直线3x+2y-3=0上.
(1)求数列{an}的通项公式;
(2)是否存在实数λ,使得数列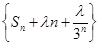 为等差数列?若存在,求出λ的值;若不存在,则说明理由.
为等差数列?若存在,求出λ的值;若不存在,则说明理由.
(1)求数列{an}的通项公式;
(2)是否存在实数λ,使得数列
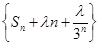 为等差数列?若存在,求出λ的值;若不存在,则说明理由.
为等差数列?若存在,求出λ的值;若不存在,则说明理由.(1) n-1(2)存在实数λ=
n-1(2)存在实数λ=
 n-1(2)存在实数λ=
n-1(2)存在实数λ=
(1)由题意可得3an+1+2Sn-3=0,①
n≥2时,3an+2Sn-1-3=0,②
①-②得3an+1-3an+2an=0,∴ =
= (n≥2),
(n≥2),
a1=1,3a2+a1-3=0,∴a2= ,∴{an}是首项为1,公比为
,∴{an}是首项为1,公比为 的等比数列,∴an=
的等比数列,∴an= n-1.
n-1.
(2)由(1)知:Sn=
若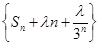 为等差数列,则S1+λ·1+
为等差数列,则S1+λ·1+ ,S2+λ·2+
,S2+λ·2+ ,S3+λ·3+
,S3+λ·3+ 成等差数列,
成等差数列,
∴2 =S1+
=S1+ λ+S3+
λ+S3+ λ,解得λ=
λ,解得λ= .
.
又λ= 时,Sn+
时,Sn+ ·n+
·n+ =
= ,显然
,显然 成等差数列,故存在实数λ=
成等差数列,故存在实数λ= ,使得数列
,使得数列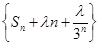 成等差数列
成等差数列
n≥2时,3an+2Sn-1-3=0,②
①-②得3an+1-3an+2an=0,∴
 =
= (n≥2),
(n≥2),a1=1,3a2+a1-3=0,∴a2=
 ,∴{an}是首项为1,公比为
,∴{an}是首项为1,公比为 的等比数列,∴an=
的等比数列,∴an= n-1.
n-1.(2)由(1)知:Sn=

若
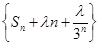 为等差数列,则S1+λ·1+
为等差数列,则S1+λ·1+ ,S2+λ·2+
,S2+λ·2+ ,S3+λ·3+
,S3+λ·3+ 成等差数列,
成等差数列,∴2
 =S1+
=S1+ λ+S3+
λ+S3+ λ,解得λ=
λ,解得λ= .
.又λ=
 时,Sn+
时,Sn+ ·n+
·n+ =
= ,显然
,显然 成等差数列,故存在实数λ=
成等差数列,故存在实数λ= ,使得数列
,使得数列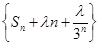 成等差数列
成等差数列
练习册系列答案
相关题目
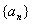 的首项
的首项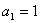 ,前
,前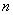 项和为
项和为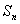 (
(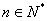 ),且点
),且点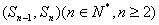 在直线
在直线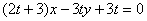 上(
上(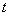 为与
为与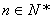 )为等比数列;
)为等比数列;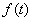 ,数列
,数列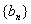 满足
满足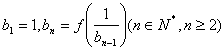 ,设
,设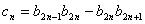 ,求数列
,求数列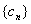 的前
的前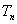 ;
;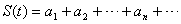 ,求函数
,求函数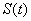 的值域.
的值域.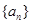 的各项均为正数,
的各项均为正数,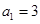 ,前
,前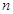 项和为
项和为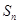 ,
,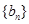 为等比数列,
为等比数列, 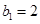 ,且
,且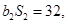
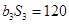 .
.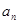 与
与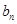 ;
; 的前
的前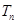 .
.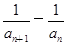 =d(n∈N*,d为常数),则称数列{an}为“调和数列”.已知正项数列
=d(n∈N*,d为常数),则称数列{an}为“调和数列”.已知正项数列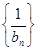 为“调和数列”,且b1+b2+…+b9=90,则b4·b6的最大值是( ).
为“调和数列”,且b1+b2+…+b9=90,则b4·b6的最大值是( ).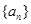 满足:当
满足:当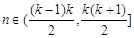 (
(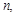
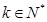 )时,
)时,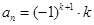 ,
,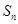 是数列
是数列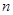 项和,定义集合
项和,定义集合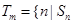 是
是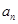 的整数倍,
的整数倍,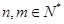 ,且
,且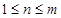
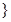 ,
,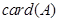 表示集合
表示集合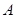 中元素的个数,则
中元素的个数,则 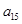 = ,
= , 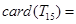 .
.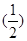 n-1=2(n∈N*),设cn=2nan.
n-1=2(n∈N*),设cn=2nan.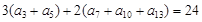 ,则该数列前13项的和是( )
,则该数列前13项的和是( )