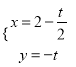Question

【题目】直线y=x+b与曲线 有且只有一个交点，则 的取值范围是 （ ）
A.
B. 或
C. 或
D.

Answer 1

【答案】B
【解析】解答：由 ，可得，曲线方程表示一个在y轴右边的单位圆的一半， 则圆心坐标为（0，0），圆的半径r=1，
画出相应的图形，如图所示：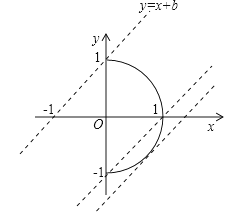

∵当直线y=x+b过（0，-1）时，把（0，-1）代入直线方程得：b=-1，
当直线y=x+b过（0，1）时，把（0，1）代入直线方程得：b=1，
∴当-1＜b≤1时，直线y=x+b与半圆只有一个交点时，
又直线y=x+b与半圆相切时，圆心到直线的距离d=r，即 ，
解得：b= （舍去）或b=- ，
综上，直线与曲线只有一个交点时，b的取值范围为-1＜b≤1或b=- ．故选B
分析：本题主要考查了直线与圆相交的性质，解决问题的关键是根据直线与圆的交点个数进行分析，利用待定系数法确定一次函数解析式，以及点到直线的距离公式；利用了数形结合的思想，根据题意得出此曲线表示在y轴右边的单位圆的一半，并画出相应的图形是解本题的关键.