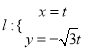题目内容
【题目】如图，已知正三棱柱ABC﹣A1B1C1的，底面边长是侧棱长2倍，D、E是A1C1、AC的中点，则下面判断不正确的为（ ）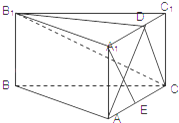 
A.直线A1E∥平面B1DC
B.直线AD⊥平面B1DC
C.平面B1DC⊥平面ACC1A1
D.直线AC与平面B1DC所成的角为60°
【答案】D
【解析】∵A1E∥DC，由线面平行的判断定理，可得直线A1E∥平面B1DC，故A正确； ∵底面边长是侧棱长2倍，∴△ADC为等腰直角三角形，即AD⊥DC，再根据直三棱柱的性质，我们易得B1D⊥平面A1ACC1 ， 进而B1D⊥AD，结合线面垂直的判断定理，可以得到直线AD⊥平面B1DC，故B正确；
结合B中结论，由面面垂直的判定定理可得平面B1DC⊥平面ACC1A1 ， 故C正确；
由B中结论，∠ACD即为直线AC与平面B1DC所成的角，∵∠ACD=45°，故D错误；
故选D
【考点精析】本题主要考查了棱柱的结构特征的相关知识点，需要掌握两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形才能正确解答此题．
快乐5加2金卷系列答案
【题目】某小区一住户在楼顶违规私自建了“阳光房”，该小区其他居民对此意见很大，通过物业和城管部门多次上门协调，该住户终于拆除了“阳光房”，对此有人认为既然已经建成再拆除太可惜了，为此业主委员会通过随机询问小区100名性别不同的居民对此件事情的看法，得到如下的2×2列联表
认为应该拆除 | 认为太可惜了 | 总计 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
总计 | 75 | 25 | 100 |
附：
P（K2≥k） | 0.10 | 0.05 | 0.025 |
k | 2.706 | 3.841 | 5.024 |
K2= 
，其中n=a+b+c+d
参照附表，由此可知下列选项正确的是（ ）
A.在犯错误的概率不超过1%的前提下，认为“是否认为拆除太可惜了与性别有关”
B.在犯错误的概率不超过1%的前提下，认为“是否认为拆除太可惜了与性别无关”
C.有90%以上的把握认为“是否认为拆除太可惜了与性别有关”
D.有90%以上的把握认为“是否认为拆除太可惜了与性别无关”
【题目】近年来我国电子商务行业迎来蓬勃发展的新机遇，网购成了大众购物的一个重要组成部分，可人们在开心购物的同时，假冒伪劣产品也在各大购物网站频频出现，为了让顾客能够在网上买到货真价实的好东西，各大购物平台也推出了对商品和服务的评价体系，现从某购物网站的评价系统中选出100次成功的交易，并对其评价进行统计，对商品的好评率为 
，对服务的好评率为 
，其中对商品和服务都做出好评的交易为30次．
（1）列出关于商品和服务评价的2×2列联表，并判断是否可以在犯错误概率不超过1%的前提下，认为商品好评与服务好评有关？
（2）若针对商品的好评率，采用分层抽样的方式从这100次交易中取出5次交易，并从中选择两次交易进行客户回访，求只有一次好评的概率．
P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（K2= 
，其中n=a+b+c+d）
