题目内容
【题目】(1)若函数![]() 的图象在
的图象在![]() 处的切线
处的切线![]() 垂直于直线
垂直于直线![]() ,求实数
,求实数![]() 的值及直线
的值及直线![]() 的方程;
的方程;
(2)求函数![]() 的单调区间;
的单调区间;
(3)若![]() ,求证:
,求证: ![]() .
.
【答案】(1)![]() ,
, ![]() ;(2)当
;(2)当![]() 时,
时, ![]() 的单调递增区间是
的单调递增区间是![]() ;当
;当![]() 时,
时, ![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】试题分析:(1)求出函数的导数,根据切线的斜率求出![]() 的值,从而求出函数的切点,点斜式求出切线方程即可;(2)求出
的值,从而求出函数的切点,点斜式求出切线方程即可;(2)求出![]() ,分别令
,分别令 ![]() 得增区间,
得增区间, ![]() 得减区间;(3)由
得减区间;(3)由![]() 时,
时, ![]() ,在
,在![]() 上单调递减,得到
上单调递减,得到![]() ,从而证明结论.
,从而证明结论.
试题解析:(1)∵![]() (
(![]() ),定义域为
),定义域为![]() ,∴
,∴![]()
∴函数![]() 的图象在
的图象在![]() 处的切线
处的切线![]() 的斜率
的斜率![]()
∵切线![]() 垂直于直线
垂直于直线![]() ,∴
,∴![]() ,∴
,∴![]()
∴![]() ,
, ![]() ,∴切点为
,∴切点为![]()
∴切线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
(2)由(1)知: ![]() ,
, ![]()
当![]() 时,
时, ![]() ,此时
,此时![]() 的单调递增区间是
的单调递增区间是![]() ;
;
当![]() 时,
时, ![]()
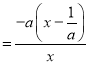
若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]()
此时![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]()
综上所述:
当![]() 时,
时, ![]() 的单调递增区间是
的单调递增区间是![]() ;
;
当![]() 时,
时, ![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .
.
(3)由(2)知:当![]() 时,
时, ![]() 在
在![]() 上单调递减
上单调递减
∴![]() 时,
时, ![]()
∴![]() 时,
时, ![]() ,即
,即![]() .
.

 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案【题目】某小区一住户在楼顶违规私自建了“阳光房”,该小区其他居民对此意见很大,通过物业和城管部门多次上门协调,该住户终于拆除了“阳光房”,对此有人认为既然已经建成再拆除太可惜了,为此业主委员会通过随机询问小区100名性别不同的居民对此件事情的看法,得到如下的2×2列联表
认为应该拆除 | 认为太可惜了 | 总计 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
总计 | 75 | 25 | 100 |
附:
P(K2≥k) | 0.10 | 0.05 | 0.025 |
k | 2.706 | 3.841 | 5.024 |
K2= ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
参照附表,由此可知下列选项正确的是( )
A.在犯错误的概率不超过1%的前提下,认为“是否认为拆除太可惜了与性别有关”
B.在犯错误的概率不超过1%的前提下,认为“是否认为拆除太可惜了与性别无关”
C.有90%以上的把握认为“是否认为拆除太可惜了与性别有关”
D.有90%以上的把握认为“是否认为拆除太可惜了与性别无关”