题目内容
18.已知∠APB=∠BPC=∠CPA=60°,则PA与平面PBC所成的角的大小为arccos$\frac{\sqrt{3}}{3}$.分析 过点A作AO垂直于平面PBC,连接PO,则PO是PA在平面PBC的射影,∠APO为PA与平面PBC所成的角,根据最小角定理,cos∠APC=cos∠CPO•cos∠APO,即可得出结论.
解答 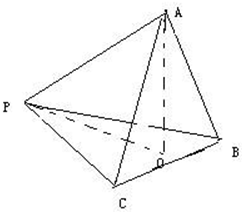 解:过点A作AO垂直于平面PBC,连接PO,则PO是PA在平面PBC的射影,∠APO为PA与平面PBC所成的角.
解:过点A作AO垂直于平面PBC,连接PO,则PO是PA在平面PBC的射影,∠APO为PA与平面PBC所成的角.
依题意得:∠CPO=30°
根据最小角定理,cos∠APC=cos∠CPO•cos∠APO
∴cos60°=cos30°•cos∠APO
∴cos∠APO=$\frac{cos60°}{cos30°}$=$\frac{\sqrt{3}}{3}$,
∴PA与平面PBC所成的角的大小为arccos$\frac{\sqrt{3}}{3}$.
故答案为:arccos$\frac{\sqrt{3}}{3}$.
点评 本题考查线面角,考查最小角定理,考查学生的计算能力,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
7.函数y=sin2x-cos2x的一条对称轴为( )
| A. | x=$\frac{π}{4}$ | B. | x=-$\frac{π}{4}$ | C. | x=$\frac{π}{8}$ | D. | x=-$\frac{π}{8}$ |
 某几何体的三视图如图所示,则该几何体的体积为$\frac{4}{3}$.
某几何体的三视图如图所示,则该几何体的体积为$\frac{4}{3}$. 如图,正方体ABCD-A1B1C1D1的棱长为1,E,F,M,N分别是A1B1,BC,C1D1,B1C1的中点.
如图,正方体ABCD-A1B1C1D1的棱长为1,E,F,M,N分别是A1B1,BC,C1D1,B1C1的中点. 如图,已知ABCD是边长为2的正方形,AF⊥平面ABCD,CE∥AF.
如图,已知ABCD是边长为2的正方形,AF⊥平面ABCD,CE∥AF. 如图,在长方体ABCD-A1B1C1D1中,A1A=$\sqrt{2}$,AD=1,DC=2,点E为AB中点.
如图,在长方体ABCD-A1B1C1D1中,A1A=$\sqrt{2}$,AD=1,DC=2,点E为AB中点.


