题目内容
【题目】据市场调查，某种商品一年内每件出厂价在6千元的基础上，按月呈
的模型波动（x为月份），已知3月份达到最高价8千元，7月份价格最低为4千元，该商品每件的售价为
（x为月份），且满足
.
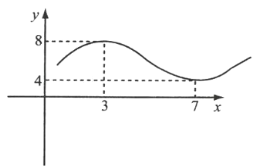
（1）分别写出该商品每件的出厂价函数
和售价函数
的解析式；
（2）问几月份的销售盈利最大？
【答案】（1）
，
；（2）6月份盈利达到最大.
【解析】
(1)由题意分别确定A,B,
和
的值即可确定函数
的解析式，然后确定函数
的解析式即可；
(2)结合(1)中的结果得到利润函数，然后结合三角函数的性质即可确定利润最大的月份.
（1）依题：A=2，B=6，T=8，
，
把点（3，8）代入可得
，
则
，
，
，
令
可得
，
所以
.
（2）设每件商品盈利为m，则：
，
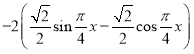
当
时，m达到最大值，
此时
,可得：
，
令
可得
.
即6月份盈利达到最大.
练习册系列答案
怎样学好牛津英语系列答案
导学教程高中新课标系列答案
相关题目
【题目】流行性感冒（简称流感）是流感病毒引起的急性呼吸道感染，是一种传染性强、传播速度快的疾病．其主要通过空气中的飞沫、人与人之间的接触或与被污染物品的接触传播．流感每年在世界各地均有传播，在我国北方通常呈冬春季流行，南方有冬春季和夏季两个流行高峰．儿童相对免疫力低，在幼儿园、学校等人员密集的地方更容易被传染．某幼儿园将去年春期该园患流感小朋友按照年龄与人数统计，得到如下数据：
年龄（ |
|
|
|
|
|
患病人数（ |
|
|
|
|
|
（1）求
关于
的线性回归方程；
（2）计算变量、的相关系数
（计算结果精确到
），并回答是否可以认为该幼儿园去年春期患流感人数与年龄负相关很强？（若
，则、相关性很强；若
，则、相关性一般；若
，则、相关性较弱．）
参考数据：
．
参考公式：
，
相关系数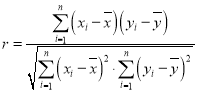
．
