题目内容
【题目】如图所示,在三棱锥![]() 中,
中,![]() 是边长为4的正三角形,平面
是边长为4的正三角形,平面![]() 平面
平面![]() ,SA=SC=
,SA=SC=![]() ,M,N分别为AB,SB的中点.
,M,N分别为AB,SB的中点.
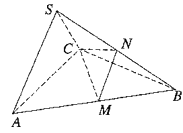
(1)求证:AC⊥SB;
(2)求二面角N-CM-B的余弦值;
【答案】(1)证明见解析;(2)![]()
【解析】
(1)取![]() ,
,![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,由题意可得
,由题意可得![]() ,
,![]() ,再由线面垂直的判定可得
,再由线面垂直的判定可得![]() 平面
平面![]() ,进一步得到
,进一步得到![]() ;
;
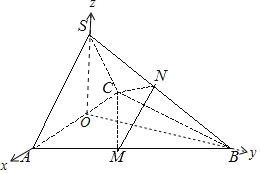
(2)如图以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系,求出
轴,建立空间直角坐标系,求出![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的坐标,得到平面
的坐标,得到平面![]() 与平面
与平面![]() 的法向量,由两法向量所成角的余弦值可得二面角
的法向量,由两法向量所成角的余弦值可得二面角![]() 的余弦值.
的余弦值.
解:(1)证明:取![]() ,
,![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,由题意可得
,由题意可得![]() ,
,![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]() ,
,
又![]() 平面
平面![]()
所以![]() ;
;
(2)解:如图以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
则![]() ,0,
,0,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,0,
,0,![]() ,
,![]() ,0,
,0,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由已知条件易得平面![]() 的法向量为
的法向量为![]() ,设面
,设面![]() 的法向量为
的法向量为![]() ,
,
![]() ,
,![]() .
.
由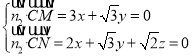 ,取
,取![]() ,得
,得![]() ,
,
设![]() 为所求角,则
为所求角,则![]() .
.
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
【题目】为提高玉米产量,某种植基地对单位面积播种数与每棵作物的产量之间的关系进行了研究,收集了![]() 块试验田的数据,得到下表:
块试验田的数据,得到下表:
试验田编号 |
|
|
|
|
|
|
|
|
|
|
|
(棵/) |
|
|
|
|
|
|
|
|
|
|
|
(斤/棵) |
|
|
|
|
|
|
|
|
|
|
|
技术人员选择模型![]() 作为
作为![]() 与
与![]() 的回归方程类型,令
的回归方程类型,令![]() ,
,![]() 相关统计量的值如下表:
相关统计量的值如下表:
|
|
|
|
|
|
|
|
由表中数据得到回归方程后进行残差分析,残差图如图所示:

(1)根据残差图发现一个可疑数据,请写出可疑数据的编号(给出判断即可,不必说明理由);
(2)剔除可疑数据后,由最小二乘法得到关于的线性回归方程![]() 中的
中的![]() ,求
,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)利用(2)得出的结果,计算当单位面积播种数![]() 为何值时,单位面积的总产量
为何值时,单位面积的总产量![]() 的预报值最大?(计算结果精确到
的预报值最大?(计算结果精确到![]() )
)
附:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() 其回归直线
其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为 ,
,![]() ,
,![]()