题目内容
【题目】已知椭圆![]() :
:![]() 的焦距为
的焦距为![]() ,且经过点
,且经过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,若椭圆上存在点
,若椭圆上存在点![]() ,使得四边形
,使得四边形![]() 为平行四边形(其中
为平行四边形(其中![]() 是坐标原点),求平行四边形
是坐标原点),求平行四边形![]() 的面积.
的面积.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由椭圆的焦距为2![]() ,且椭圆C过点
,且椭圆C过点![]() ,列出方程求出a,b,由此能求出椭圆C的方程;(2)设直线
,列出方程求出a,b,由此能求出椭圆C的方程;(2)设直线![]() 的方程为
的方程为![]() ,由
,由 ,消去
,消去![]() 得
得
![]() .利用韦达定理可得
.利用韦达定理可得![]() ,点P在椭圆上可得
,点P在椭圆上可得![]() 表示平行四边形
表示平行四边形![]() 的面积即可.
的面积即可.
解:(1)由题意可知椭圆的左、右焦点分别为![]() ,
,![]() ,
,
又椭圆![]() 经过点
经过点![]() ,所以
,所以![]() ,
,
即![]() ,
,
所以![]() ,即
,即![]() ,
,
又![]() ,所以椭圆的标准方程为
,所以椭圆的标准方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,由
,由 ,消去
,消去![]() 得
得
![]() .设
.设![]() ,
,![]() ,
,![]() ,
,
则有![]() ,即
,即![]() ,
,
又![]() ,
,![]() .
.
因为四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,故
,故![]() ,
,
![]()
![]() ,
,
所以![]() ,
,
由点![]() 在椭圆上可得
在椭圆上可得 ,化简得
,化简得![]()
而![]()
![]() .
.
又因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]() .
.
又点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
故![]() 的面积
的面积![]() .
.
所以平行四边形![]() 的面积为
的面积为![]() .
.

【题目】为提高玉米产量,某种植基地对单位面积播种数与每棵作物的产量之间的关系进行了研究,收集了![]() 块试验田的数据,得到下表:
块试验田的数据,得到下表:
试验田编号 |
|
|
|
|
|
|
|
|
|
|
|
(棵/) |
|
|
|
|
|
|
|
|
|
|
|
(斤/棵) |
|
|
|
|
|
|
|
|
|
|
|
技术人员选择模型![]() 作为
作为![]() 与
与![]() 的回归方程类型,令
的回归方程类型,令![]() ,
,![]() 相关统计量的值如下表:
相关统计量的值如下表:
|
|
|
|
|
|
|
|
由表中数据得到回归方程后进行残差分析,残差图如图所示:

(1)根据残差图发现一个可疑数据,请写出可疑数据的编号(给出判断即可,不必说明理由);
(2)剔除可疑数据后,由最小二乘法得到关于的线性回归方程![]() 中的
中的![]() ,求
,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)利用(2)得出的结果,计算当单位面积播种数![]() 为何值时,单位面积的总产量
为何值时,单位面积的总产量![]() 的预报值最大?(计算结果精确到
的预报值最大?(计算结果精确到![]() )
)
附:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() 其回归直线
其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为 ,
,![]() ,
,![]()
【题目】为打赢脱贫攻坚战,解决脱贫问题,政府重点扶持扶贫工厂.当地对某扶贫工厂进行设备改造,为分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取100件产品作为样本,检测质量指标值![]() .该产品为次品、合格品、优等品所对应的指标值范围分别为
.该产品为次品、合格品、优等品所对应的指标值范围分别为![]() ,
,![]() ,
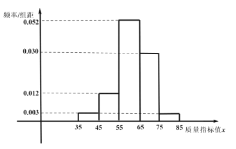
,![]() .设备改造前的样本的频率分布直方图如图所示,设备改造后的样本的频数分布表如下所示.
.设备改造前的样本的频率分布直方图如图所示,设备改造后的样本的频数分布表如下所示.
质量指标值 |
|
|
|
|
|
频数 | 1 | 4 | 47 | 38 | 10 |
(Ⅰ)根据以上数据,完成以下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为设备改造与产品为次品有关?
的把握认为设备改造与产品为次品有关?
次品 | 非次品 | 合计 | |
改造前 | |||
改造后 | |||
合计 |
(Ⅱ)若工人的月工资是由基本工资1000元与效益工资两部分组成.效益工资实施细则如下:每生产一件产品是合格品的奖50元,是优等品的奖100元,是次品的扣20元.将频率视为概率,估计设备改造后,一个月生产60件产品的工人月工资为多少元?
附:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
![]()