题目内容
【题目】![]() 的内角
的内角![]() ,
,![]() ,
,![]() 所对的边分别为
所对的边分别为![]() ,
,![]() ,
,![]() ,已知
,已知![]() .
.
(Ⅰ)求![]() ;
;
(Ⅱ)若![]() ,且
,且![]() 的面积为
的面积为![]() ,求
,求![]() 的周长.
的周长.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
解法一:(I)运用正弦定理和正弦两角和公式,处理式子,计算B的大小,即可。(II)结合三角形面积计算公式,得到![]() 的大小,运用余弦定理,计算b,即可。解法二:(I)运用余弦定理,处理原式,计算角B的大小,即可(II)结合三角形面积计算公式,计算ac的值,结合已知条件,计算a,c的大小,结合余弦定理,得到b的大小,计算周长,即可。
的大小,运用余弦定理,计算b,即可。解法二:(I)运用余弦定理,处理原式,计算角B的大小,即可(II)结合三角形面积计算公式,计算ac的值,结合已知条件,计算a,c的大小,结合余弦定理,得到b的大小,计算周长,即可。
解法一:
(Ⅰ)在![]() 中,
中,
∵![]() ,
,
∴![]() ,
,
得![]() ,
,
即![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() .
.
(Ⅱ)依题意得![]() ,
,
∵![]() ,∴
,∴![]() ,
,
得![]() .
.
又![]() ,
,
∴![]()
![]() ,
,
得![]() ,
,
∴![]() 的周长为
的周长为![]() .
.
解法二:(Ⅰ)在![]() 中,
中,
∵![]() ,
,
∴![]() ,
,
化简得![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() .
.
(Ⅱ)依题意得![]() ,
,
∵![]() ,∴
,∴![]() ,
,
得![]() .
.
又![]() ,
,
解得![]() 或
或![]() .
.
∴![]() ,
,
得![]() ,
,
∴![]() 的周长为
的周长为![]() .
.

 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案【题目】为提高玉米产量,某种植基地对单位面积播种数与每棵作物的产量之间的关系进行了研究,收集了![]() 块试验田的数据,得到下表:
块试验田的数据,得到下表:
试验田编号 |
|
|
|
|
|
|
|
|
|
|
|
(棵/) |
|
|
|
|
|
|
|
|
|
|
|
(斤/棵) |
|
|
|
|
|
|
|
|
|
|
|
技术人员选择模型![]() 作为
作为![]() 与
与![]() 的回归方程类型,令
的回归方程类型,令![]() ,
,![]() 相关统计量的值如下表:
相关统计量的值如下表:
|
|
|
|
|
|
|
|
由表中数据得到回归方程后进行残差分析,残差图如图所示:

(1)根据残差图发现一个可疑数据,请写出可疑数据的编号(给出判断即可,不必说明理由);
(2)剔除可疑数据后,由最小二乘法得到关于的线性回归方程![]() 中的
中的![]() ,求
,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)利用(2)得出的结果,计算当单位面积播种数![]() 为何值时,单位面积的总产量
为何值时,单位面积的总产量![]() 的预报值最大?(计算结果精确到
的预报值最大?(计算结果精确到![]() )
)
附:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() 其回归直线
其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为 ,
,![]() ,
,![]()
【题目】为打赢脱贫攻坚战,解决脱贫问题,政府重点扶持扶贫工厂.当地对某扶贫工厂进行设备改造,为分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取100件产品作为样本,检测质量指标值![]() .该产品为次品、合格品、优等品所对应的指标值范围分别为
.该产品为次品、合格品、优等品所对应的指标值范围分别为![]() ,
,![]() ,
,![]() .设备改造前的样本的频率分布直方图如图所示,设备改造后的样本的频数分布表如下所示.
.设备改造前的样本的频率分布直方图如图所示,设备改造后的样本的频数分布表如下所示.
质量指标值 |
|
|
|
|
|
频数 | 1 | 4 | 47 | 38 | 10 |
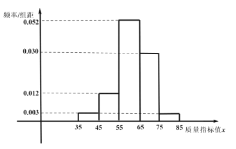
(Ⅰ)根据以上数据,完成以下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为设备改造与产品为次品有关?
的把握认为设备改造与产品为次品有关?
次品 | 非次品 | 合计 | |
改造前 | |||
改造后 | |||
合计 |
(Ⅱ)若工人的月工资是由基本工资1000元与效益工资两部分组成.效益工资实施细则如下:每生产一件产品是合格品的奖50元,是优等品的奖100元,是次品的扣20元.将频率视为概率,估计设备改造后,一个月生产60件产品的工人月工资为多少元?
附:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
![]()
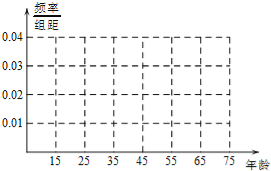
【题目】今年年初,我国多个地区发生了持续性大规模的雾霾天气,给我们的身体健康产生了巨大的威胁.私家车的尾气排放也是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
(Ⅰ)完成被调查人员的频率分布直方图;
(Ⅱ)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行进行追踪调查,记选中的4人中不赞成“车辆限行”的人数为ξ,求随机变量ξ的分布列和数学期望.