题目内容
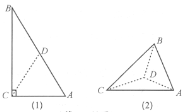
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]()
![]() ,
,![]() 是斜边
是斜边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折,若在翻折过程中存在某个位置,使得
翻折,若在翻折过程中存在某个位置,使得![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
由已知条件推导出,![]() ,BC=x,取BC中点E,翻折前
,BC=x,取BC中点E,翻折前![]() ,翻折后
,翻折后![]() ,从而求出
,从而求出![]() .翻折后,当△B1CD与△ACD在一个平面上,∠A=60°,BC=ACtan60°,此时
.翻折后,当△B1CD与△ACD在一个平面上,∠A=60°,BC=ACtan60°,此时![]() ,由此能求出x的取值范围为(0,
,由此能求出x的取值范围为(0,![]() ].
].
由题意得,![]() ,BC=x,取BC中点E,
,BC=x,取BC中点E,
翻折前,在图1中,连接DE,CD,则![]() ,
,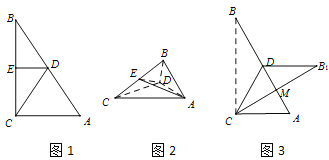
翻折后,在图2中,此时CB⊥AD.
∵BC⊥DE,BC⊥AD,∴BC⊥平面ADE,
∴BC⊥AE,DE⊥BC,
又BC⊥AE,E为BC中点,∴AB=AC=1,
∴![]() ,
,
在△ADE中:①![]() ,②
,②![]() ,③x>0;
,③x>0;
由①②③可得![]() .
.
如图3,翻折后,当△B1CD与△ACD在一个平面上,
AD与B1C交于M,且AD⊥B1C,AD=B1D=CD=BD,∠CBD=∠BCD=∠B1CD,
又∠CBD+∠BCD+∠B1CD=90°,
∴∠CBD=∠BCD=∠B1CD=30°,
∴∠A=60°,BC=ACtan60°,此时![]() ,
,
综上,x的取值范围为![]() .
.
故选:D.

【题目】某贫困地区共有1500户居民,其中平原地区1050户,山区450户.为调查该地区2017年家庭收入情况,从而更好地实施“精准扶贫”,采用分层抽样的方法,收集了150户家庭2017年年收入的样本数据(单位:万元).

(1)应收集多少户山区家庭的样本数据?
(2)根据这150个样本数据,得到2017年家庭收入的频率分布直方图(如图所示),其中样本数据分组区间为(0,0.5],(0.5,1],(1,1.5],(1.5,2],(2,2.5],(2.5,3].如果将频率视为概率,估计该地区2017年家庭收入超过1.5万元的概率;
(3)样本数据中,有5户山区家庭的年收入超过2万元,请完成2017年家庭收入与地区的列联表,并判断是否有90%的把握认为“该地区2017年家庭年收入与地区有关”?
超过2万元 | 不超过2万元 | 总计 | |
平原地区 | |||
山区 | 5 | ||
总计 |
附:
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
【题目】为打赢脱贫攻坚战,解决脱贫问题,政府重点扶持扶贫工厂.当地对某扶贫工厂进行设备改造,为分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取100件产品作为样本,检测质量指标值![]() .该产品为次品、合格品、优等品所对应的指标值范围分别为
.该产品为次品、合格品、优等品所对应的指标值范围分别为![]() ,
,![]() ,
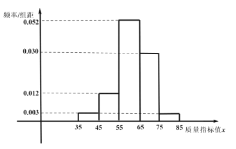
,![]() .设备改造前的样本的频率分布直方图如图所示,设备改造后的样本的频数分布表如下所示.
.设备改造前的样本的频率分布直方图如图所示,设备改造后的样本的频数分布表如下所示.
质量指标值 |
|
|
|
|
|
频数 | 1 | 4 | 47 | 38 | 10 |
(Ⅰ)根据以上数据,完成以下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为设备改造与产品为次品有关?
的把握认为设备改造与产品为次品有关?
次品 | 非次品 | 合计 | |
改造前 | |||
改造后 | |||
合计 |
(Ⅱ)若工人的月工资是由基本工资1000元与效益工资两部分组成.效益工资实施细则如下:每生产一件产品是合格品的奖50元,是优等品的奖100元,是次品的扣20元.将频率视为概率,估计设备改造后,一个月生产60件产品的工人月工资为多少元?
附:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
![]()