题目内容
【题目】如图,四棱锥 ![]() ,底面
,底面 ![]() 为菱形,
为菱形, ![]() 平面
平面 ![]() ,
, ![]() ,
, ![]() 为
为 ![]() 的中点,
的中点, ![]() .
.
(I)求证:直线 ![]() 平面
平面 ![]() ;
;
(II)求直线 ![]() 与平面
与平面 ![]() 所成角的正弦值.
所成角的正弦值.
【答案】(I)证明: ![]() ,
,![]()
又 ![]()
又 ![]() 平面
平面 ![]() ,
, ![]()
![]() 直线
直线 ![]() 平面
平面 ![]() .
.
(II)(方法一)连接 ![]() 过
过 ![]() 点作
点作 ![]() 于
于 ![]() 点.
点.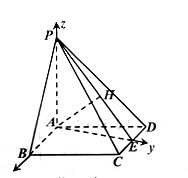
![]() ,
,![]() 平面
平面 ![]() ,
, ![]()
![]() .
.
又 ![]() ,
, ![]() 平面
平面 ![]() .
.
所以 ![]() 为直线
为直线 ![]() 与平面
与平面 ![]() 所成的角.
所成的角.
在 ![]() 中,
中, ![]() ,
, ![]()
![]() 直线
直线 ![]() 与平面
与平面 ![]() 所成角的正弦值为
所成角的正弦值为 ![]()
(方法二)如图建立所示的空间直角坐标系 ![]() .
.![]() .
.![]()
设平面 ![]() 的法向量
的法向量 ![]() ,
,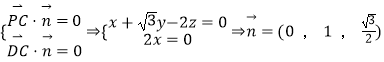
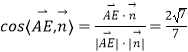 .所以直线
.所以直线 ![]() 与平面
与平面 ![]() 所成角的正弦值为
所成角的正弦值为 ![]()
【解析】(I)推导出AE⊥CD,AE⊥AB,从而PA⊥AE,由此能证明直线AE⊥平面PAB.
(II)(方法一)连接PE,过A点作AH⊥PE于H点,推导出∠AEP为直线AE与平面PCD所成的角,推导出直线AE与平面PCD所成角的正弦值.
(方法二)建立所示的空间直角坐标系A-xyz,由此利用向量法能求出直线AE与平面PCD所成角的正弦值.
【考点精析】本题主要考查了空间中直线与平面之间的位置关系的相关知识点,需要掌握直线在平面内—有无数个公共点;直线与平面相交—有且只有一个公共点;直线在平面平行—没有公共点才能正确解答此题.

【题目】心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取 ![]() 名同学(男
名同学(男 ![]() 人,女
人,女 ![]() 人),给所有同学几何题和代数题各一题,让各位同学只能自由选择其中一道题进行解答.选题情况如下表(单位:人):
人),给所有同学几何题和代数题各一题,让各位同学只能自由选择其中一道题进行解答.选题情况如下表(单位:人):
几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
附表及公式: ![]()

(1)能否据此判断有 ![]() 的把握认为视觉和空间能力与性别有关?
的把握认为视觉和空间能力与性别有关?
(2)现从选择做几何题的 ![]() 名女生中,任意抽取两人,对她们的答题情况进行全程研究,记甲、乙两位女生被抽到的人数为
名女生中,任意抽取两人,对她们的答题情况进行全程研究,记甲、乙两位女生被抽到的人数为 ![]() ,求
,求 ![]() 的分布列和
的分布列和 ![]() .
.