题目内容
4.已知函数f(x)=ex-ax,a∈R.(Ⅰ)若函数f(x)在x=0处的切线过点(1,0),求a的值;
(Ⅱ)若函数f(x)在(-1,+∞)上不存在零点,求a的取值范围;
(Ⅲ)若a=1,设函数$g(x)=\frac{1}{f(x)+ax}+\frac{4x}{{{e^x}-f(x)+4}}$,求证:当x≥0时,g(x)≥1.
分析 (Ⅰ)求得函数的导数,求得切线的斜率,由两点的斜率公式,解方程可得a;
(Ⅱ)由题意可得a=$\frac{{e}^{x}}{x}$在x>-1无解,设h(x)=$\frac{{e}^{x}}{x}$,求得导数,单调区间和极值,即可得到a的范围;
(Ⅲ)a=1,化简函数g(x)=$\frac{1}{{e}^{x}}$+$\frac{4x}{x+4}$,当x≥0时,g(x)≥1等价为ex(3x-4)+x+4≥0,令F(x)=ex(3x-4)+x+4,求出导数,判断单调性即可得证.
解答 解:(Ⅰ)f(x)=ex-ax的导数为f′(x)=ex-a,
函数f(x)在x=0处的切线斜率为1-a,
在x=0处的切线过点(1,0),可得1-a=-1,
解得a=2;
(Ⅱ)函数f(x)在(-1,+∞)上不存在零点,即为
a=$\frac{{e}^{x}}{x}$在x>-1无解,设h(x)=$\frac{{e}^{x}}{x}$,
即有h′(x)=$\frac{{e}^{x}(x-1)}{{x}^{2}}$,
当-1<x<0,或0<x<1时,h′(x)<0,h(x)递减;
当x>1时,h′(x)>0,h(x)递增.
则x>0时,x=1处h(x)取得最小值e,-1<x<0时,h(x)<-$\frac{1}{e}$.
则有a的范围是-$\frac{1}{e}$≤a<e;
(Ⅲ)证明:a=1,函数$g(x)=\frac{1}{f(x)+ax}+\frac{4x}{{{e^x}-f(x)+4}}$=$\frac{1}{{e}^{x}}$+$\frac{4x}{x+4}$,
当x≥0时,g(x)≥1等价为ex(3x-4)+x+4≥0,
令F(x)=ex(3x-4)+x+4,F(0)=0,F′(x)=ex(3x-1)+1,F′(0)=0,
再令G(x)=ex(3x-1)+1,G′(x)=ex(3x+2)>0,
即有G(x)在x≥0递增,即为G(x)≥G(0)=0,
即有F′(x)≥0,即F(x)在x≥0递增,
则F(x)≥F(0)=0,即有ex(3x-4)+x+4≥0,
故当x≥0时,g(x)≥1.
点评 本题考查导数的运用:求切线的斜率和单调区间、极值,考查函数方程的转化思想和不等式的证明,注意运用构造函数,求得单调性解决,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | 16 | B. | 18 | C. | 36 | D. | 48 |
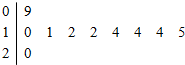 10名工人某天生产同一零件,生产的件数茎叶图如图所示,若众数为c,则c=( )
10名工人某天生产同一零件,生产的件数茎叶图如图所示,若众数为c,则c=( )| A. | 12 | B. | 14 | C. | 15 | D. | 17 |
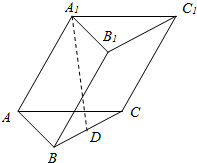 如图,斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,D是BC的中点,A1D⊥平面ABC.
如图,斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,D是BC的中点,A1D⊥平面ABC.