题目内容
已知某校5个学生的数学和物理成绩如下表
（1）假设在对这
名学生成绩进行统计时，把这名学生的物理成绩搞乱了，数学成绩没出现问题，问：恰有
名学生的物理成绩是自己的实际分数的概率是多少？
（2）通过大量事实证明发现，一个学生的数学成绩和物理成绩具有很强的线性相关关系的，在上述表格是正确的前提下，用
表示数学成绩，用
表示物理成绩，求与的回归方程；
（3）利用残差分析回归方程的拟合效果，若残差和在
范围内，则称回归方程为“优拟方程”，问：该回归方程是否为“优拟方程”.
参考数据和公式：
，其中
，
；
,残差和公式为：
（1）假设在对这
名学生成绩进行统计时，把这名学生的物理成绩搞乱了，数学成绩没出现问题，问：恰有名学生的物理成绩是自己的实际分数的概率是多少？（2）通过大量事实证明发现，一个学生的数学成绩和物理成绩具有很强的线性相关关系的，在上述表格是正确的前提下，用
表示数学成绩，用表示物理成绩，求与的回归方程；（3）利用残差分析回归方程的拟合效果，若残差和在
范围内，则称回归方程为“优拟方程”，问：该回归方程是否为“优拟方程”.参考数据和公式：
，其中，；,残差和公式为：（1）
；（2）
；（3）为”优拟方程”
；（2）；（3）为”优拟方程”本试题主要是考查了线性回归方程的求解以及优拟方程的求解问题。
（1）记事件
为恰好有两个是自己的实际分，则有古典概型概率可知为
（2）先求解
，以及b的值，然后得到a的值，进而得到方程的求解。
解：（1）记事件为恰好有两个是自己的实际分，———————4分
（2），——————————5分
，
，—————————7分
回归直线方程为—————8分
（3）
，——————————11分
所以为”优拟方程”————————12分
（1）记事件
为恰好有两个是自己的实际分，则有古典概型概率可知为（2）先求解
，以及b的值，然后得到a的值，进而得到方程的求解。解：（1）记事件
为恰好有两个是自己的实际分，———————4分（2）
，——————————5分，，—————————7分回归直线方程为
—————8分（3）
，——————————11分所以为”优拟方程”————————12分
练习册系列答案
阅读快车系列答案
相关题目
和房屋的面积
的数据： 
时的销售价格.
， 
，
，
）
与销售额
之间有如下的对应数据： 
～
月份用水量（单位：百吨）的一组数据：
，则据此模型预测6月份用水量为________百吨
=20.87，根据这一数据分析，我们有_______的把握认为打鼾与患心脏病是______ 的. 
线性相关系数为
线性相关系数为
线性相关系数为
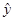=0.7x+0.35，那么表中m的值为（ ）