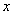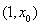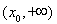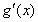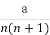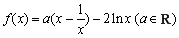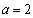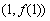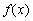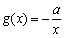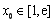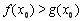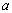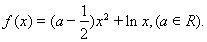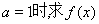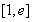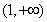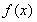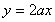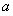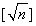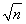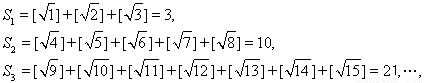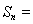题目内容
已知函数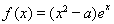 .
.
(Ⅰ)若函数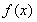 在
在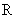 上不是单调函数,求实数
上不是单调函数,求实数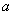 的取值范围;
的取值范围;
(Ⅱ)当 时,讨论函数
时,讨论函数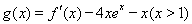 的零点个数.
的零点个数.
(Ⅰ) (Ⅱ)只有一个零点
(Ⅱ)只有一个零点
【解析】(Ⅰ)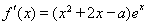 ,由题意知方程
,由题意知方程 有两个不同的实数解,
有两个不同的实数解,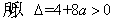 ,解得
,解得 .因此,实数
.因此,实数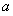 的取值范围是
的取值范围是 .--------6分
.--------6分
(Ⅱ) ,
,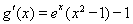 .--------7分
.--------7分
设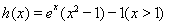 ,
,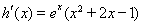 ,
,
因为 ,所以
,所以 ,故
,故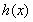 在
在 上是增函数,---------9分
上是增函数,---------9分
又 ,
,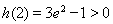 ,
,
因此在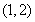 内存在唯一的实数
内存在唯一的实数 ,使得
,使得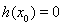 ,--------------11分
,--------------11分
因为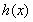 在
在 上市增函数,所以在
上市增函数,所以在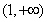 内存在唯一的实数
内存在唯一的实数 ,使得
,使得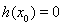 .
.
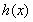 与
与 随
随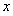 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
| 极小值 |
|
由上表可知,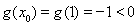 ,又
,又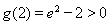 ,
,
故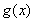 的大致图象右图所示:
的大致图象右图所示:

所以函数 在
在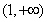 内只有一个零点. --------15分
内只有一个零点. --------15分

练习册系列答案
相关题目
为了解某班学生喜爱打篮球是否与性别有关,对该班50名学生进行了问卷调查,得到了如下的2×2列联表:
| 喜爱打篮球 | 不喜爱打篮球 | 总计 |
男生 | 20 | 5 | 25 |
女生 | 10 | 15 | 25 |
总计 | 30 | 20 | 50 |
则在犯错误的概率不超过 的前提下认为喜爱打篮球与性别有关(请用百分数表示).
附:χ2=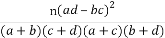
P(χ2≥x0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
x0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |