题目内容
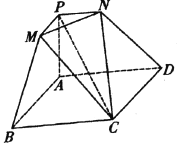
【题目】(2018·长沙二模)在平面几何中有如下结论：正三角形ABC的内切圆面积为S1，外接圆面积为S2，则
.推广到空间可以得到类似结论：已知正四面体P－ABC的内切球体积为V1，外接球体积为V2，则
＝________.
【答案】
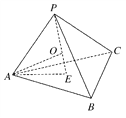
【解析】由平面图形类比空间图形，由二维类比三维，如图，设正四面体P－ABC的棱长为a，E为等边三角形ABC的中心，O为内切球与外接球的球心，则AE＝
a，PE＝
a.设OA＝R，OE＝r，则r＝a－R，又在Rt△AOE中，OA2＝OE2＋AE2，即R2＝
2＋
2，∴R＝
a，r＝
a，∴正四面体的外接球和内切球的半径之比是31，故正四面体P－ABC的内切球体积V1与外接球体积V2之比等于127，即
＝
.
练习册系列答案
相关题目
