题目内容
已知函数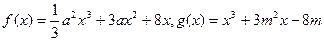 ,
,
(1)求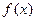 在x=1处的切线斜率的取值范围;
在x=1处的切线斜率的取值范围;
(2)求当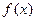 在x=1处的切线的斜率最小时,
在x=1处的切线的斜率最小时,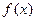 的解析式;
的解析式;
(3)在(Ⅱ)的条件下,是否总存在实数m,使得对任意的 ,总存在
,总存在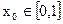 ,使得
,使得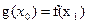 成立?若存在,求出实数m的取值范围;若不存在,说明理由.
成立?若存在,求出实数m的取值范围;若不存在,说明理由.
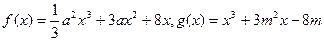 ,
,(1)求
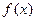 在x=1处的切线斜率的取值范围;
在x=1处的切线斜率的取值范围;(2)求当
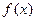 在x=1处的切线的斜率最小时,
在x=1处的切线的斜率最小时,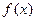 的解析式;
的解析式;(3)在(Ⅱ)的条件下,是否总存在实数m,使得对任意的
 ,总存在
,总存在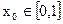 ,使得
,使得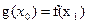 成立?若存在,求出实数m的取值范围;若不存在,说明理由.
成立?若存在,求出实数m的取值范围;若不存在,说明理由.(1) (2)
(2)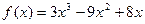 (3)存在,
(3)存在,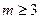
 (2)
(2)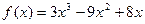 (3)存在,
(3)存在,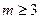
(1)
所以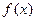 在x=1处的切线斜率的取值范围为
在x=1处的切线斜率的取值范围为
(2)由(1)知 ,则
,则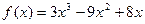
(3)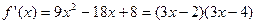 ,则有
,则有
所以当 时,
时,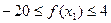 ,假设对任意的
,假设对任意的 都存在
都存在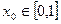 使得
使得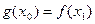 成立,设
成立,设 的最大值为T,最小值为t,则
的最大值为T,最小值为t,则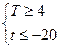
又 ,所以当
,所以当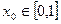 时,
时, 且
且 ,所以
,所以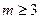 .
.

所以
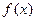 在x=1处的切线斜率的取值范围为
在x=1处的切线斜率的取值范围为
(2)由(1)知
 ,则
,则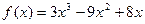
(3)
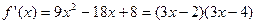 ,则有
,则有 | x | -1 | 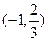 |  |  |  | 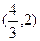 | 2 |
 | | + | 0 | - | 0 | + | |
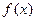 | -20s | 增 | 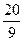 | 减 |  | 增 | 4 |
所以当
 时,
时,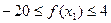 ,假设对任意的
,假设对任意的 都存在
都存在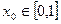 使得
使得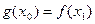 成立,设
成立,设 的最大值为T,最小值为t,则
的最大值为T,最小值为t,则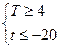
又
 ,所以当
,所以当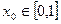 时,
时, 且
且 ,所以
,所以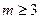 .
. 
练习册系列答案
相关题目
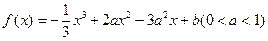
 ,求a的取值范围.
,求a的取值范围.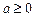 ,
,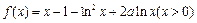 .令
.令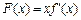 ,讨论
,讨论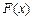 在
在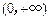 内的单调性并求极值;
内的单调性并求极值;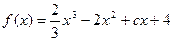 ,
,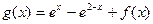 ,
,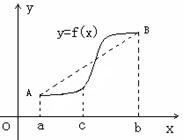
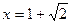 处取得极值,试求c的值和f(x)的单调增区间;
处取得极值,试求c的值和f(x)的单调增区间;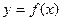 的图象在
的图象在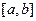 连续光滑,试猜想拉格朗日中值定理:即一定存在
连续光滑,试猜想拉格朗日中值定理:即一定存在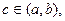 使得
使得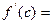 ?(用含有a,b,f(a),f(b)的表达式直接回答)
?(用含有a,b,f(a),f(b)的表达式直接回答)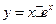 的最小值为 。
的最小值为 。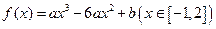 的最大值为
的最大值为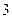 ,最小值为
,最小值为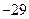 ,求
,求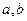 。
。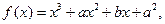 在
在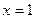 时有极值
时有极值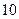 ,那么
,那么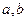 的值分别为_
的值分别为_ 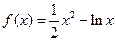 的最小值为 .
的最小值为 .