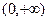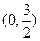题目内容
设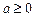 ,
,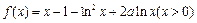 .令
.令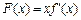 ,讨论
,讨论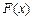 在
在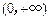 内的单调性并求极值;
内的单调性并求极值;
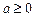 ,
,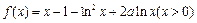 .令
.令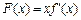 ,讨论
,讨论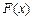 在
在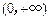 内的单调性并求极值;
内的单调性并求极值;知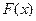 在
在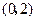 内是减函数,在
内是减函数,在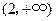 内是增函数,
内是增函数,  处取得极小值
处取得极小值 .
.
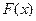 在
在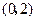 内是减函数,在
内是减函数,在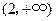 内是增函数,
内是增函数,  处取得极小值
处取得极小值 .
.根据求导法则有 ,
,
故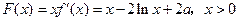 ,于是
,于是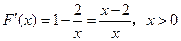 ,
,
列表如下:
故知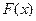 在
在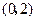 内是减函数,在
内是减函数,在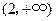 内是增函数,所以,在
内是增函数,所以,在 处取得极小值
处取得极小值 .
.
 ,
,故
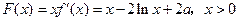 ,于是
,于是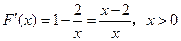 ,
, | 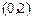 | 2 | 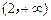 |
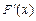 | 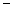 | 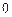 | 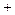 |
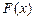 | 减 | 极小值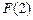 | 增 |
故知
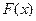 在
在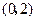 内是减函数,在
内是减函数,在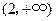 内是增函数,所以,在
内是增函数,所以,在 处取得极小值
处取得极小值 .
.
练习册系列答案
相关题目
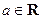 ,若函数
,若函数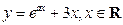 有大于零的极值点,则
有大于零的极值点,则



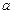 为实数,函数
为实数,函数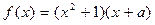 ,若
,若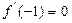 ,求函数
,求函数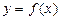 在
在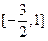 上的最大值和最小值。
上的最大值和最小值。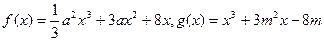 ,
,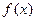 在x=1处的切线斜率的取值范围;
在x=1处的切线斜率的取值范围; ,总存在
,总存在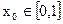 ,使得
,使得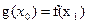 成立?若存在,求出实数m的取值范围;若不存在,说明理由.
成立?若存在,求出实数m的取值范围;若不存在,说明理由.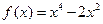 有( )
有( )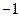 ,极大值
,极大值
 ,极大值
,极大值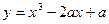 在
在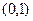 内有极小值,则实数
内有极小值,则实数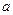 的取值范围为( )
的取值范围为( )