题目内容
在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:1,2,3,4,5
| 编号n | 1 | 2 | 3 | 4 | 5 |
| 成绩xn | 70 | 76 | 72 | 70 | 72 |
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
(注:方差s2=
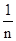 [(x1-
[(x1- )2+(x2-
)2+(x2- )2+…+(xn-
)2+…+(xn- )2],其中
)2],其中 为x1,x2,…,xn的平均数)
为x1,x2,…,xn的平均数)
(1) s=7;(2)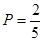
解析试题分析:(1)根据平均数的计算公式,可直接求解;(2)本题考查古典概型概率求法,关键是 正确求出基本事件总数和所求事件包含基本事件数,要做到不重不漏,例:从5个不同小球中,取出2个小球,有三种取法:
①同时取:10种取法;②依次取,取后不放回:20种取法;③依次取,取后放回:25种取法.
试题解析:(1)∵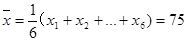
∴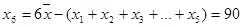 2分
2分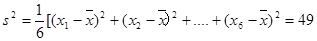 4分
4分
∴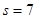 .
.
(2)从5位同学中随机选取2位同学,共有如下10种不同的取法:
{1,2},{1,3},{1,4},{1,5},{2,3},{2,4},{2,5},{3,4},{3,5},{4,5}. 7分
选出的2位同学中,恰有1位同学的成绩位于(68,75)的取法共有如下4种:
{1,2},{2,3},{2,4},{2,5}. 10分
故所求概率为 . 12分
. 12分
考点:概率和统计.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
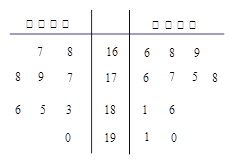
海淀课时新作业金榜卷系列答案学校为了使运动员顺利参加运动会,招募了8名男志愿者和12名女志愿者,这20名志愿者的身高如下茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
| 男 | | 女 | ||||||
| | | 8 | 16 | 5 | 8 | 9 | | |
| 8 | 7 | 6 | 17 | 2 | 3 | 5 | 5 | 6 |
| 7 | 4 | 2 | 18 | 0 | 1 | 2 | | |
| | | 1 | 19 | 0 | | | | |
(Ⅱ)若从所有“高个子”中随机选3名志愿者,用
 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出 的分布列,并求
的分布列,并求 的数学期望.
的数学期望. 一个袋子中装有6个红球和4个白球,假设每一个球被摸到的可能性是相等的.
(Ⅰ)从袋子中摸出3个球,求摸出的球为2个红球和1个白球的概率;
(Ⅱ)从袋子中摸出两个球,其中白球的个数为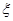 ,求
,求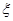 的分布列和数学期望.
的分布列和数学期望.
某校50名学生参加智力答题活动,每人回答3个问题,答对题目个数及对应人数统计结果见下表:
| 答对题目个数 | 0 | 1 | 2 | 3 |
| 人数 | 5 | 10 | 20 | 15 |
(Ⅰ)从50名学生中任选两人,求两人答对题目个数之和为4或5的概率;
(Ⅱ)从50名学生中任选两人,用X表示这两名学生答对题目个数之差的绝对值,求随机变量X的分布列及数学期望EX.
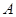 饮料,另外2杯为
饮料,另外2杯为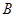 饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯
饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯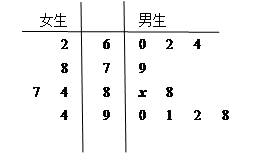
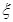 ,求
,求