题目内容
一个袋子中装有6个红球和4个白球,假设每一个球被摸到的可能性是相等的.
(Ⅰ)从袋子中摸出3个球,求摸出的球为2个红球和1个白球的概率;
(Ⅱ)从袋子中摸出两个球,其中白球的个数为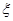 ,求
,求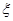 的分布列和数学期望.
的分布列和数学期望.
(Ⅰ)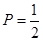 ;(Ⅱ)见解析.
;(Ⅱ)见解析.
解析试题分析:(Ⅰ)先求出从袋中摸3个球的总事件数,再求出摸到的球是2个红球1个白球的事件数,做比值即可;(Ⅱ)先求出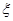 取相应值时对应的概率,再列出分布列求期望.
取相应值时对应的概率,再列出分布列求期望.
试题解析:解:(Ⅰ)从装有10个球的袋子中摸出3个球的事件总数为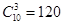 ,
,
其中摸出的三个球有2个红球1个白球的事件总数为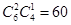 ,
,
所以所求的概率为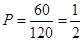 ; 4分
; 4分
(Ⅱ)从10个球的袋子里摸出2个球的事件总数为 ,
,
2个球都不是白球的概率为 ,
,
1个白球1个红球的概率为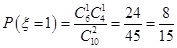 ,
,
2个都是白球的概率为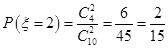 , 8分
, 8分
所以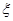 的分布列为:
的分布列为:
10分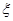


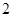
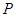
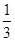
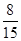
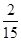
所以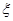 的数学期望为
的数学期望为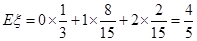 14分
14分
考点:1、等可能事件及其概率;2、随机变量的分布列与期望.

练习册系列答案
相关题目
某品牌的汽车4S店,对最近100位采用分期付款的购车者进行统计,统计结果如下表所示:
| 付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 40 | 20 | 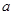 | 10 | 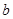 |
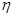 表示经销一辆汽车的利润.
表示经销一辆汽车的利润.(1)求上表中
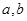 的值;
的值;(2)若以频率作为概率,求事件
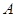 :“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率
:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率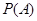 ;(3)求
;(3)求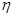 的分布列及数学期望
的分布列及数学期望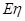 .
. 在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:1,2,3,4,5
| 编号n | 1 | 2 | 3 | 4 | 5 |
| 成绩xn | 70 | 76 | 72 | 70 | 72 |
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
(注:方差s2=
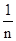 [(x1-
[(x1- )2+(x2-
)2+(x2- )2+…+(xn-
)2+…+(xn- )2],其中
)2],其中 为x1,x2,…,xn的平均数)
为x1,x2,…,xn的平均数) 某小组共有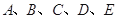 五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)如下表所示:
五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)如下表所示:
| | A | B | C | D | E |
| 身高 | 1.69 | 1.73 | 1.75 | 1.79 | 1.82 |
| 体重指标 | 19.2 | 25.1 | 18.5 | 23.3 | 20.9 |
(2)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的概率.
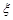 表示游客在甲、乙、丙三处旅游景点中选择游玩的景点数和没有选择游玩的景点数的乘积.
表示游客在甲、乙、丙三处旅游景点中选择游玩的景点数和没有选择游玩的景点数的乘积.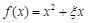 是R上的偶函数”为事件A,求事件A的概率;
是R上的偶函数”为事件A,求事件A的概率;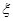 的概率分布列及数学期望.
的概率分布列及数学期望. 、
、 ,记
,记 .
. 取最大值的概率;
取最大值的概率;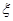 为取得红球的个数.
为取得红球的个数. 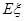 .
.