题目内容
某饮料公司对一名员工进行测试以便确定其考评级别.公司准备了两种不同的饮料共5 杯,其颜色完全相同,并且其中3杯为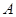 饮料,另外2杯为
饮料,另外2杯为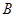 饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯
饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯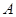 饮料.若该员工3杯都选对,则评为优秀;若3杯选对2杯,则评为良好;否则评为及格.假设此人对
饮料.若该员工3杯都选对,则评为优秀;若3杯选对2杯,则评为良好;否则评为及格.假设此人对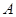 和
和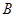 两种饮料没有鉴别能力.
两种饮料没有鉴别能力.
(Ⅰ)求此人被评为优秀的概率;
(Ⅱ)求此人被评为良好及以上的概率.
(Ⅰ)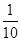 ;(Ⅱ)
;(Ⅱ)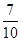 .
.
解析试题分析:根据古典概型的两个特点(基本事件的有限性和每个基本事件发生的等可能性)判断本题属于古典概型,古典概型中,求事件发生的概率,先要求出基本事件数,再求出所求概率事件包含的基本事件数,相比即可.
试题解析:从5杯饮料中任选3杯,所有的选法有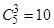 (种)
(种)
(Ⅰ)设“此人被评为优秀”为事件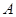 ,即“选中3杯
,即“选中3杯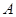 饮料”这个事件发生了,这个事件包含的基本事件数为
饮料”这个事件发生了,这个事件包含的基本事件数为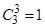 (种),所以事件
(种),所以事件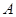 发生的概率为
发生的概率为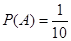 .
.
(Ⅱ)设“此人被评为良好及以上”为事件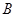 ,即“选中3杯
,即“选中3杯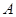 饮料或选中2杯
饮料或选中2杯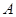 饮料”这个事件发生了,这个事件包含的基本事件数为
饮料”这个事件发生了,这个事件包含的基本事件数为 (种),所以事件
(种),所以事件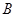 发生的概率为
发生的概率为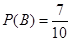 .
.
考点:组合数的计算、古典概型.

练习册系列答案
相关题目
一中食堂有一个面食窗口,假设学生买饭所需的时间互相独立,且都是整数分钟,对以往学生买饭所需的时间统计结果如下:
| 买饭时间(分) | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
(Ⅰ)估计第三个学生恰好等待4分钟开始买饭的概率;
(Ⅱ)
 表示至第2分钟末已买完饭的人数,求
表示至第2分钟末已买完饭的人数,求 的分布列及数学期望
的分布列及数学期望 气象部门提供了某地今年六月份(30天)的日最高气温的统计表如下:
| 日最高气温t (单位:℃) | t 22℃ 22℃ | 22℃< t 28℃ 28℃ | 28℃< t  32℃ 32℃ | 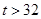 ℃ ℃ |
| 天数 | 6 | 12 |  |  |
 和
和 数据不清楚,但气象部门提供的资料显示,六月份的日最高气温不高于32℃的频率为0.9.
数据不清楚,但气象部门提供的资料显示,六月份的日最高气温不高于32℃的频率为0.9.(Ⅰ) 若把频率看作概率,求
 ,
, 的值;
的值;(Ⅱ) 把日最高气温高于32℃称为本地区的 “高温天气”,根据已知条件完成下面
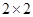 列联表,并据此你是否有95%的把握认为本地区的“高温天气”与西瓜“旺销”有关?说明理由.
列联表,并据此你是否有95%的把握认为本地区的“高温天气”与西瓜“旺销”有关?说明理由.| | 高温天气 | 非高温天气 | 合计 |
| 旺销 | 1 | | |
| 不旺销 | | 6 | |
| 合计 | | | |

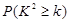 | 0.10 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
某市 、
、 、
、 、
、 四所中学报名参加某高校今年自主招生的学生人数如下表所示:
四所中学报名参加某高校今年自主招生的学生人数如下表所示:
| 中学 |  |  |  |  |
| 人数 |  |  |  |  |
 名参加问卷调查.
名参加问卷调查.(1)问
 、
、 、
、 、
、 四所中学各抽取多少名学生?
四所中学各抽取多少名学生?(2)从参加问卷调查的
 名学生中随机抽取两名学生,求这两名学生来自同一所中学的概率;
名学生中随机抽取两名学生,求这两名学生来自同一所中学的概率;(3)在参加问卷调查的
 名学生中,从来自
名学生中,从来自 、
、 两所中学的学生当中随机抽取两名学生,用
两所中学的学生当中随机抽取两名学生,用 表示抽得
表示抽得 中学的学生人数,求
中学的学生人数,求 的分布列.
的分布列. 在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:1,2,3,4,5
| 编号n | 1 | 2 | 3 | 4 | 5 |
| 成绩xn | 70 | 76 | 72 | 70 | 72 |
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
(注:方差s2=
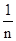 [(x1-
[(x1- )2+(x2-
)2+(x2- )2+…+(xn-
)2+…+(xn- )2],其中
)2],其中 为x1,x2,…,xn的平均数)
为x1,x2,…,xn的平均数) 
 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求 、
、 ,记
,记 .
. 取最大值的概率;
取最大值的概率; 为选取女生的人数,求X的分布列及数学期望.
为选取女生的人数,求X的分布列及数学期望. ,求
,求 、
、 、
、 三个局商上任,求
三个局商上任,求