题目内容
为了了解某班的男女生学习体育的情况,按照分层抽样分别抽取了10名男生和5名女生作为样本,他们期末体育成绩的茎叶图如图所示,其中茎为十位数,叶为个位数。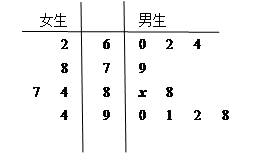
(Ⅰ)若该班男女生平均分数相等,求x的值;
(Ⅱ)若规定85分以上为优秀,在该10名男生中随机抽取2名,优秀的人数记为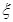 ,求
,求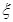 的分布列和数学期望.
的分布列和数学期望.
(Ⅰ)6;(Ⅱ) .
.
解析试题分析:(Ⅰ)平均数公式为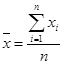 ;(Ⅱ)
;(Ⅱ)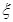 的可能取值为0,1,2,求出相应的概率,得到分布列,应用期望公式
的可能取值为0,1,2,求出相应的概率,得到分布列,应用期望公式 求出期望.
求出期望.
试题解析:(Ⅰ)依题意可得,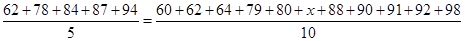 , 1分
, 1分
∴x=6. 3分
(Ⅱ)由茎叶图可知,10名男生中优秀的人数为6人。 4分
∴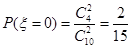 , 6分
, 6分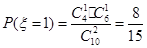 , 8分
, 8分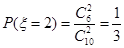 , 10分
, 10分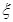
0 1 2 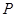

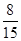
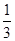
∴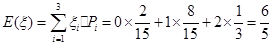 .
.
答: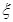 的数学期望为
的数学期望为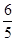 . 12分.
. 12分.
考点:随机事件的概率和随机变量的分布列、数学期望等概念.

在某校高三学生的数学校本课程选课过程中,规定每位同学只能选一个科目.已知某班第一小组与第二小组各有六位同学选择科目甲或科目乙,情况如下表:
| | 科目甲 | 科目乙 | 总计 |
| 第一小组 | 1 | 5 | 6 |
| 第二小组 | 2 | 4 | 6 |
| 总计 | 3 | 9 | 12 |
(1)求选出的4人均选科目乙的概率;
(2)设
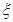 为选出的4个人中选科目甲的人数,求
为选出的4个人中选科目甲的人数,求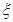 的分布列和数学期望.
的分布列和数学期望. 在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:1,2,3,4,5
| 编号n | 1 | 2 | 3 | 4 | 5 |
| 成绩xn | 70 | 76 | 72 | 70 | 72 |
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
(注:方差s2=
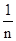 [(x1-
[(x1- )2+(x2-
)2+(x2- )2+…+(xn-
)2+…+(xn- )2],其中
)2],其中 为x1,x2,…,xn的平均数)
为x1,x2,…,xn的平均数) 某经销商试销A、B两种商品一个月(30天)的记录如下:
| 日销售量(件) | 0 | 1 | 2 | 3 | 4 | 5 |
| 商品A的频数 | 2 | 5 | 7 | 7 | 5 | 4 |
| 商品B的频数 | 4 | 4 | 6 | 8 | 5 | 3 |
(Ⅰ)求B商品日销售量不超过3件的概率;
(Ⅱ)由于某种原因,该商家决定只选择经销A、B商品的一种,你认为应选择哪种商品,说明理由。
 、
、 ,记
,记 .
. 取最大值的概率;
取最大值的概率; 为选取女生的人数,求X的分布列及数学期望.
为选取女生的人数,求X的分布列及数学期望.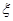 为取得红球的个数.
为取得红球的个数.  .
.