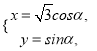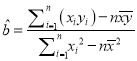题目内容
【题目】在平面直角坐标系中,以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为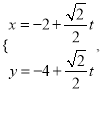 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)直角坐标方程为![]() ,普通方程为
,普通方程为![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)本题考察的是极坐标系下的方程和参数方程与平面直角坐标系下的方程的互化,只需记清楚公式,计算时要细心。
本题的解题思路是将参数代入曲线![]() 的直角坐标系的方程,得到关于参数
的直角坐标系的方程,得到关于参数![]() 的一元二次方程
的一元二次方程
,再利用直线参数方程中![]() 的几何意义和韦达定理,结合题目所给的等量关系,建立关于
的几何意义和韦达定理,结合题目所给的等量关系,建立关于![]() 的方程,即可求出
的方程,即可求出![]() 的值.此类题目很容易忽略参数方程中
的值.此类题目很容易忽略参数方程中![]() 的几何意义,一定要明白参数
的几何意义,一定要明白参数![]() 在参数方程中所在的地位和意义。
在参数方程中所在的地位和意义。
试题解析:(1)由![]() 得
得![]()
∴曲线![]() 的直角坐标方程为
的直角坐标方程为![]()
直线![]() 的普通方程为
的普通方程为![]()
(2)将直线![]() 的参数方程代入曲线
的参数方程代入曲线![]() 的直角坐标方程
的直角坐标方程![]() 中,
中,
得![]()
设![]() 两点对应的参数分别为
两点对应的参数分别为![]()
则有![]()
![]()
∵![]() ,∴
,∴![]() 即
即![]()
∴![]() 即
即![]()
解之得: ![]() 或者
或者![]() (舍去),∴
(舍去),∴![]() 的值为1
的值为1

【题目】某校的一个社会实践调查小组,在对该校学生的良好“用眼习惯”的调查中,随机发放了120分问卷.对收回的100份有效问卷进行统计,得到如![]() 下列联表:
下列联表:
做不到科学用眼 | 能做到科学用眼 | 合计 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
合计 | 75 | 25 | 100 |
(1)现按女生是否能做到科学用眼进行分层,从45份女生问卷中抽取了6份问卷,从这6份问卷中再随机抽取3份,并记其中能做到科学用眼的问卷的份数![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若在犯错误的概率不超过![]() 的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的
的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的![]() 的值应为多少?请说明理由.
的值应为多少?请说明理由.
附:独立性检验统计量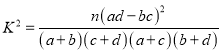 ,其中
,其中![]() .
.
独立性检验临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
【题目】某校计划面向高一年级1240名学生开设校本选修课程,为确保工作的顺利实施,按性别进行分层抽样,现抽取124名学生对社会科学类、自然科学类这两大类校本选修课程进行选课意向调查,其中男生有65人.在这124名学生中选修社会科学类的男生有22人、女生有40人.
(1)根据以上数据完成下列列联表;
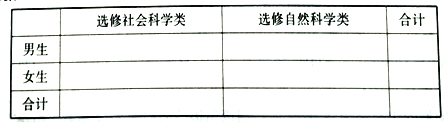
(2)判断能否有99.9%的把握认为科类的选修与性别有关?
附: 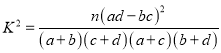 ,其中
,其中![]()
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |