题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() ,求函数
,求函数![]() 的单调区间.
的单调区间.
【答案】(1)![]() ;(2)
;(2)![]() 在
在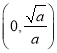 单调递减,在
单调递减,在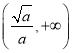 单调递增.
单调递增.
【解析】试题分析:(1)求导数,利用导数的几何意义曲线![]() 在点
在点![]() 处的切线斜率
处的切线斜率![]() 的值,根据点斜式可得切线方程;(2)先求出函数的导数,根据
的值,根据点斜式可得切线方程;(2)先求出函数的导数,根据![]() 解关于
解关于![]() 导函数的不等式可得增区间,
导函数的不等式可得增区间, ![]() 解关于
解关于![]() 的不等式,可求出函数的单调减区间.
的不等式,可求出函数的单调减区间.
试题解析:(1)当![]() 时,函数
时,函数![]() ,
, ![]() ,
,
∴![]() ,
,
∴曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(2)![]() .
.
令![]() ,解得
,解得![]() ;
;
令![]() ,解得
,解得![]() ;
;
∴![]() 在
在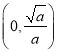 单调递减,在
单调递减,在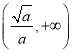 单调递增.
单调递增.
【方法点晴】本题主要考查利用导数求曲线切线以及及利用导数研究函数的单调性,属于中档题.求曲线切线方程的一般步骤是:(1)求出![]() 在
在![]() 处的导数,即
处的导数,即![]() 在点
在点![]()
![]() 出的切线斜率(当曲线
出的切线斜率(当曲线![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行时,在 处导数不存在,切线方程为
轴平行时,在 处导数不存在,切线方程为![]() );(2)由点斜式求得切线方程
);(2)由点斜式求得切线方程![]() .
.

练习册系列答案
相关题目
【题目】某市英才中学的一个社会实践调查小组,在对中学生的良好“光盘习惯”的调查中,随机发放了120份问卷,对收回的120份有效问卷进行统计,得到如下![]() 列联表:
列联表:
做不到光盘 | 能做到光盘 | 合计 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
合计 | 75 | 25 | 100 |
(1)现已按是否能做到光盘分层从45份女生问卷中抽取9份问卷,若从这9份问卷中随机抽取4份,并记其中能做到光盘的问卷的份数为![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)如果认为良好“光盘习惯”与性别有关犯错误的概率不超过![]() ,那么根据临界值表最精确的
,那么根据临界值表最精确的![]() 的值应为多少?请说明理由.
的值应为多少?请说明理由.
附:独立性检验统计量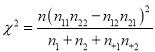 ,其中
,其中![]() .
.
独立性检验临界表:
|
|
|
|
|
|
|
|
|
|
|
|