题目内容
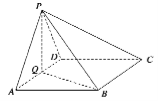
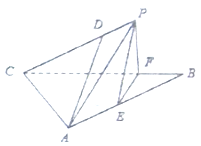
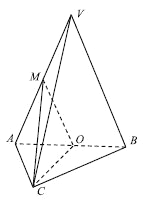
【题目】如图,在三棱锥![]() 中,平面
中,平面![]()
![]() 平面
平面![]() ,
, ![]() ,
, ![]() 且
且![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.
的中点.
(1)求证: ![]()
![]() 平面
平面![]() ;
;
(2)求证:平面![]()
![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.
【答案】(1)证明过程见解析;(2)证明过程见解析;(3)![]()
【解析】试题分析:(1)通过中位线的性质证明线线平行,再通过线线平行证明线面平行;(2)通过证明![]() ,进而证明
,进而证明![]() ⊥平面
⊥平面![]() ,再通过线面垂直证明面面垂直;(3)求三棱锥
,再通过线面垂直证明面面垂直;(3)求三棱锥![]() 的体积时,观察将哪个面作为底面比较合适,较容易求出,通过前面两问的铺垫,发现将面
的体积时,观察将哪个面作为底面比较合适,较容易求出,通过前面两问的铺垫,发现将面![]() 作为底面较为合适,从而可求解.
作为底面较为合适,从而可求解.
试题解析:
(1)证明: ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,
的中点,
∵![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2) ![]()
![]() ,且
,且![]() 是
是![]() 的中点,∴
的中点,∴![]() .
.
又平面![]() ⊥平面
⊥平面![]() ,
,
∴![]() ⊥平面
⊥平面![]() ,
,
又![]() 平面
平面![]() ,
,
∴平面![]() ⊥平面
⊥平面![]() .
.
(3) 因为![]() ,且
,且![]() ,
,
所以![]()
连![]() ,又
,又![]() , 所以
, 所以![]()
由(2)知: ![]() ⊥平面
⊥平面![]() ,
,
∴![]()

【题目】为了分析某个高三学生的学习状态,对其下一阶段的学习提供指导性建议.现对他前![]() 次考试的数学成绩
次考试的数学成绩![]() 、物理成绩进行分析.下面是该生
、物理成绩进行分析.下面是该生![]() 次考试的成绩.
次考试的成绩.
数学 | 108 | 103 | 137 | 112 | 128 | 120 | 132 |
物理 | 74 | 71 | 88 | 76 | 84 | 81 | 86 |
(Ⅰ)他的数学成绩与物理成绩哪个更稳定?请给出你的说明;
(Ⅱ)已知该生的物理成绩![]() 与数学成绩是线性相关的,求物理成绩
与数学成绩是线性相关的,求物理成绩![]() 与数学成绩的回归直线方程
与数学成绩的回归直线方程
(Ⅲ)若该生的物理成绩达到90分,请你估计他的数学成绩大约是多少?
(附: 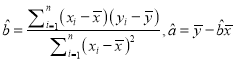 )
)
【题目】甲、乙两企业生产同一种型号零件,按规定该型号零件的质量指标值落在![]() 内为优质品.从两个企业生产的零件中各随机抽出了500件,测量这些零件的质量指标值,得结果如下表:
内为优质品.从两个企业生产的零件中各随机抽出了500件,测量这些零件的质量指标值,得结果如下表:
甲企业:

乙企业:

(1)已知甲企业的500件零件质量指标值的样本方差![]() ,该企业生产的零件质量指标值
,该企业生产的零件质量指标值![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为质量指标值的样本平均数
近似为质量指标值的样本平均数![]() (注:求
(注:求![]() 时,同一组数据用该区间的中点值作代表),
时,同一组数据用该区间的中点值作代表),![]() 近似为样本方差
近似为样本方差![]() ,试根据该企业的抽样数据,估计所生产的零件中,质量指标值不低于71.92的产品的概率.(精确到0.001)
,试根据该企业的抽样数据,估计所生产的零件中,质量指标值不低于71.92的产品的概率.(精确到0.001)
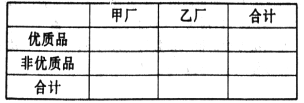
(2)由以上统计数据完成下面![]() 列联表,并问能否在犯错误的概率不超过0.01的前提下,认为“两个分厂生产的零件的质量有差异”.
列联表,并问能否在犯错误的概率不超过0.01的前提下,认为“两个分厂生产的零件的质量有差异”.
附注:
参考数据: ![]() ,
,
参考公式: ![]() ,
, ![]() ,
,
![]() .
.
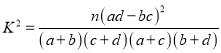
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |