Question

【题目】已知函数（为自然对数的底数）.

（1）求函数的单调区间；

（2）当时，若对任意的恒成立，求实数的值；

（3）求证：.

Answer 1

【答案】（Ⅰ）时，单调递增区间为；时，单调递减区间为，

单调递增区间为；（Ⅱ）；（Ⅲ）证明见解析

【解析】

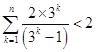试题分析：（1）先求导函数数，利用，即可求函数的单调增区间，即可求函数的单调减区间；（2）若对任意的恒成立，对恒成立, 即可求实数的值；（3）要证原不等式成立，只需证：，即证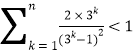：，结合（2）利用裂项相消法求和，根据放缩法可证．

试题解析：解：（1），∴时，，在上单调递增：时，时，单调递减，时，单调递增．

（2）由（1），时，，∴，即，

记．，∴在上增，在上递减，∴，故，得．

（3）时，，时，，

时，．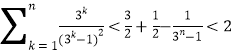

由（2）可知，即，则时，，故，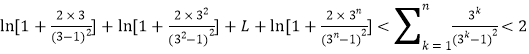

即原不等式成立．