题目内容
(本题满分12分)
已知函数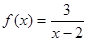 .
.
(1)判断该函数在区间(2,+∞)上的单调性,并给出证明;
(2)求该函数在区间[3,6]上的最大值和最小值.
已知函数
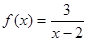 .
.(1)判断该函数在区间(2,+∞)上的单调性,并给出证明;
(2)求该函数在区间[3,6]上的最大值和最小值.
(1)在区间(2,+∞)是减函数,证明:x1,x2是区间上的任意两个实数,且x1<x2,f(x1)-f(x2)= 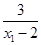 -
-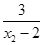 =
=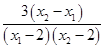 由2< x1 <x2得f (x1)-f (x2)>0,所以函数
由2< x1 <x2得f (x1)-f (x2)>0,所以函数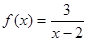 在区间(2,+∞)是减函数(2)最大值3,最小值
在区间(2,+∞)是减函数(2)最大值3,最小值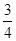
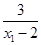 -
-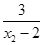 =
=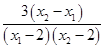 由2< x1 <x2得f (x1)-f (x2)>0,所以函数
由2< x1 <x2得f (x1)-f (x2)>0,所以函数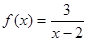 在区间(2,+∞)是减函数(2)最大值3,最小值
在区间(2,+∞)是减函数(2)最大值3,最小值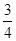
试题分析:(1)函数
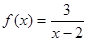 在区间(2,+∞)是减函数 …………2分
在区间(2,+∞)是减函数 …………2分证明:设x1,x2是区间上的任意两个实数,且x1<x2,则
f(x1)-f(x2)=
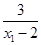 -
-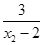 =
=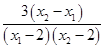 …………4分
…………4分由2< x1 <x2,得x2-x1>0,( x1-2) ( x2-2)>0
于是f (x1)-f (x2)>0,f (x1)>f (x2)
函数
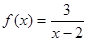 在区间(2,+∞)是减函数. …………8分
在区间(2,+∞)是减函数. …………8分(2)由可知
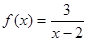 在区间[3,6]的两个端点上分别取得最大值和最小值,即当x=3时取得最大值3,当x=6时取得最小值
在区间[3,6]的两个端点上分别取得最大值和最小值,即当x=3时取得最大值3,当x=6时取得最小值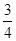 . …………12分
. …………12分点评:定义法判定单调性的步骤:1,所给区间取
 ,2,计算
,2,计算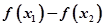 ,3,判定差值的正负号,4,得到函数单调性
,3,判定差值的正负号,4,得到函数单调性
练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
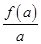 ,
, 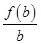 ,
,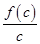 的大小关系是
的大小关系是  ,
, 是常数)在x=e处的切线方程为
是常数)在x=e处的切线方程为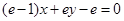 ,
,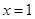 既是函数
既是函数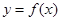 的零点,又是它的极值点.
的零点,又是它的极值点.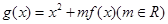 在区间(1,3)内不是单调函数,求实数m的取值范围;
在区间(1,3)内不是单调函数,求实数m的取值范围; 的单调递减区间,并证明:
的单调递减区间,并证明: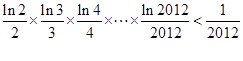
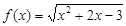 的递减区间是 。
的递减区间是 。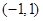 上的函数
上的函数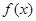 满足:对任意
满足:对任意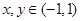 ,
,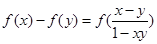 恒成立.有下列结论:①
恒成立.有下列结论:①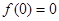 ;②函数
;②函数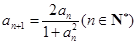 ,且
,且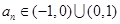 ,则数列
,则数列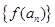 为等比数列.
为等比数列.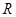 上的函数
上的函数 ,如果存在函数
,如果存在函数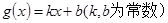 ,使得
,使得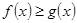 对一切实数
对一切实数 都成立,则称
都成立,则称 是函数
是函数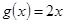 是
是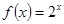 的一个“亲密函数”;
的一个“亲密函数”;