某班的全体学生参加数学测试.成绩的频率分布直方图如图.数据的分组依次为:[20.40).[40.60).[60.80).[80.100].依此表可以估计这次测试成绩的中位数为70分．(1)求表中a.b的值,(2)请估计该班本次数学测试的平均分．题目和参考答案——青夏教育精英家教网—

题目内容

17．

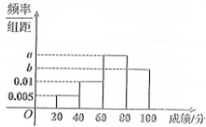某班的全体学生（共50人）参加数学测试（百分制），成绩的频率分布直方图如图，数据的分组依次为：[20，40），[40，60），[60，80），[80，100]，依此表可以估计这次测试成绩的中位数为70分．
（1）求表中a，b的值；
（2）请估计该班本次数学测试的平均分．

分析（1）根据频率分布直方图，和频率=$\frac{频数}{总数}$，即可求出，
（2）根据平均数定义即可求得．

解答解：（1）由中位数为70可得0.005×20+0.01×20+a×10=0.5，
解得a=0.02，
又20（0.005+0.01+0.02+b）=1，解得b=0.015，
（2）该班本次数学测试的平均成绩估计值为30×0.1+50×0.2+70×0.4+90×0.3=68分．

点评本题题考查了学生的识图及计算能力，频率分布直方图的性质，及平均数的定义，属于基础题．

练习册系列答案

8．

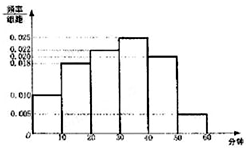电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况，随机抽取了100名观众进行调查，其中女性有55名．下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图；
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”，已知“体育迷”中有10名女性．
（Ⅰ）根据已知条件完成下面的2×2列联表

	非体育迷	体育迷	合计
男
女
合计

（Ⅱ）将日均收看该体育项目不低于50分钟的观众称为“超级体育迷”，已知“超级体育迷”中有2名女性，若从“超级体育迷”中任意选取2人，求至少有1名女性观众的概率．

5．已知函数f（x）=x³-3ax-1（a∈R）
（1）试讨论函数f（x）的单调区间；
（2）若f（x）=0在x∈[0，1]上恒成立，求a的取值范围．

12．

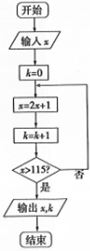如图所示的程序框图中，若输入x的值为10，则输出的x与k的值的和为（　　）

2．集合M={x|x=sin$\frac{nπ}{3}$，n∈Z}，N={x|x=cos$\frac{nπ}{2}$，n∈N}，M∩N等于（　　）

9．若函数f（x）=x-$\frac{2}{x}$-3lnx+k在其定义域上有三个零点，则实数k的取值范围是（　　）

6．已知f（α）=$\frac{{cos（{3π+α}）cos（{\frac{3π}{2}+α}）sin（{-α}）}}{{tan（{-π-α}）sin（{3π-α}）cos（{-π-α}）}}$．
（1）化简f（α）；
（2）已知角α为锐角，$f（{α+\frac{π}{6}}）=\frac{3}{5}$，求f（α）的值．

7．已知向量$\overrightarrow{m}$=（4sinx，1），$\overrightarrow{n}$=（cos（x+$\frac{π}{6}$），1）
（Ⅰ）设函数f（x）=$\overrightarrow{m}$•$\overrightarrow{n}$，求函数f（x）在区间[0，$\frac{π}{2}$]上的最大值和最小值；
（Ⅱ）若f（$\frac{A}{2}$）=$\frac{6}{5}$，$\frac{π}{3}$＜A＜$\frac{5}{6}$π，求cos2A的值．

试题分类