题目内容
【题目】如图所示,在四棱锥P-ABCD中,底面是边长为1的正方形,侧棱PD=1,PA=PC=![]() .
.
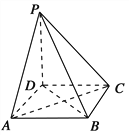
(1)求证:PD⊥平面ABCD;
(2)求证:平面PAC⊥平面PBD;
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)由题意及图形利用线面垂直的判定定理即可得证;(2)由(1)可得PD⊥AC,又四边形ABCD为正方形,所以AC⊥BD,由线面垂直的判定定理得到AC⊥平面PBD,进一步利用面面垂直的判断证明;
试题解析:(1)∵PD=1,DC=1,PC=![]() ,
,
∴PC2=PD2+DC2,
∴PD⊥DC.
同理可证PD⊥AD,又AD∩DC=D,
∴PD⊥平面ABCD.
(2)由(1)知PD⊥平面ABCD,
∴PD⊥AC,而四边形ABCD是正方形,
∴AC⊥BD,又BD∩PD=D,
∴AC⊥平面PDB.
同时,AC平面PAC,
∴平面PAC⊥平面PBD.

练习册系列答案
相关题目